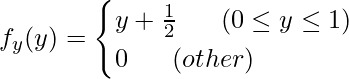- Step1. 基礎編
- 15. いろいろな確率分布3
15-5. 2変数の確率分布
確率変数がとる値とその値をとる確率の対応を表したものが「確率分布」であることは11-1章で既に学びました。この章では、確率変数が2つある場合に、それぞれの確率変数がとる値とその確率の分布を表す「同時確率分布」について学びます。確率変数が離散型である場合には「離散型同時確率分布」といい、確率変数が連続型である場合には「連続型同時確率分布」といいます。
■離散型同時確率分布
あるクラスの生徒40人の血液型を集計した次のようなデータについて考えます。
| A型 | O型 | B型 | AB型 | 計 | |
|---|---|---|---|---|---|
| 男子 | 10 | 4 | 4 | 2 | 20 |
| 女子 | 8 | 8 | 2 | 2 | 20 |
上の表をそれぞれ割合(確率)に書き換えてみます。例えば、男子でA型の生徒の確率は10/40=0.25になります。
| A型 | O型 | B型 | AB型 | |
|---|---|---|---|---|
| 男子 | 0.25 | 0.1 | 0.1 | 0.05 |
| 女子 | 0.2 | 0.2 | 0.05 | 0.05 |
このように2つの離散型確率変数![]() と
と![]() がそれぞれある値をとるときの確率を表したものを「同時確率分布」といいます。
がそれぞれある値をとるときの確率を表したものを「同時確率分布」といいます。![]() が
が![]() を、
を、![]() が
が![]() をとるときの同時確率分布は
をとるときの同時確率分布は
と表します。また、![]() を「同時確率関数」といいます。確率の総和は必ず1になるので、同時確率分布に関して次の式が成り立ちます。
を「同時確率関数」といいます。確率の総和は必ず1になるので、同時確率分布に関して次の式が成り立ちます。
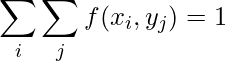
次に、それぞれの確率変数をとる確率の合計を算出してみます。
| A型 | O型 | B型 | AB型 | 計 | |
|---|---|---|---|---|---|
| 男子 | 0.25 | 0.1 | 0.1 | 0.05 | 0.5 |
| 女子 | 0.2 | 0.2 | 0.05 | 0.05 | 0.5 |
| 計 | 0.45 | 0.3 | 0.15 | 0.1 | 1 |
この表を見ると、A型の合計確率は0.45、O型の合計確率は0.3であることが分ります。このように、ある1つの確率変数を抜き出して(それ以外の確率変数は無視して)、その確率の総和を求めたものを「周辺確率分布」といいます。![]() が
が![]() を、
を、![]() が
が![]() をとるときの周辺確率分布は、
をとるときの周辺確率分布は、
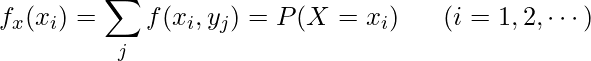
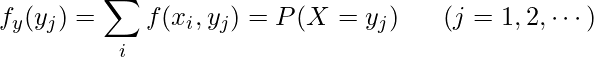
と表します。![]() と
と![]() をそれぞれ
をそれぞれ![]() と
と![]() の「周辺確率関数」といいます。
の「周辺確率関数」といいます。
■連続型同時確率分布
![]() と
と![]() がそれぞれ連続型確率変数である場合、
がそれぞれ連続型確率変数である場合、![]() と
と![]() の同時確率分布を表す関数を「同時確率密度関数」といい、
の同時確率分布を表す関数を「同時確率密度関数」といい、![]() で表します。同時確率密度関数を使うと、
で表します。同時確率密度関数を使うと、![]() となる確率
となる確率![]() を求めることができます。
を求めることができます。
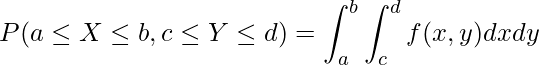
確率の総和は必ず1になるので、同時確率密度関数に関して次の式が成り立ちます。
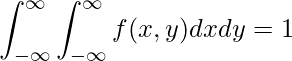
また、![]() と
と![]() それぞれの「周辺確率密度関数」である
それぞれの「周辺確率密度関数」である![]() と
と![]() は次の式から求められます。
は次の式から求められます。
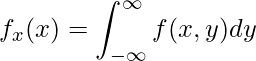
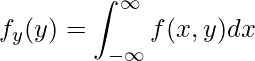
例えば、次のような同時確率密度関数について考えてみます。
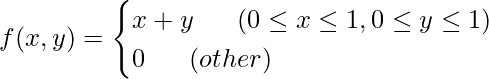
この式から、![]() となる確率を求めると次のようになります。
となる確率を求めると次のようになります。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle P(0 \leq x \leq \frac{1}{2}, 0 \leq y \leq \frac{1}{2}) &=&\int_0^\frac{1}{2} \int_0^\frac{1}{2} {(x+y)dxdy} \\ &=&\int_0^\frac{1}{2}{\left[\frac{1}{2}x^2+yx\right]_0^\frac{1}{2}dy}\\ &=&\int_0^\frac{1}{2}{\left(\frac{1}{8}+\frac{1}{2}y\right)dy}\\ &=&\left[\frac{1}{8}y+\frac{1}{4}y^2\right]_0^\frac{1}{2}\\ &=&\frac{1}{16}+\frac{1}{16}=\frac{1}{8} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-c0d7ea4318f70df22bae8c4337909b28_l3.png)
![]() の周辺確率密度関数を求めてみます。
の周辺確率密度関数を求めてみます。![]() の範囲では、
の範囲では、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle f_x(x) &=&\int_{0}^{1} {f(x,y)dy} \\ &=&\int_{0}^{1} {(x+y)dy} \\ &=&\left[xy+\frac{1}{2}y^2 \right]_0^1 \\ &=&x+\frac{1}{2} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-39f71becfcd59b11f070b2123805ad70_l3.png)
と計算できるので、まとめると次のようになります。
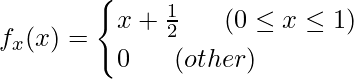
![]() の周辺確率密度関数も同様に計算できます。
の周辺確率密度関数も同様に計算できます。