- Step1. 基礎編
- 15. いろいろな確率分布3
15-3. 連続一様分布1
15-2章では離散一様分布について説明しましたが、この章では連続一様分布について説明します。確率変数![]() がどのような値でも、その時の確率密度関数
がどのような値でも、その時の確率密度関数![]() が一定の値をとる分布のことを連続一様分布といいます。コンピュータを使うと、連続一様分布の乱数を簡単に得ることが出来ます。確率変数
が一定の値をとる分布のことを連続一様分布といいます。コンピュータを使うと、連続一様分布の乱数を簡単に得ることが出来ます。確率変数![]() が
が![]() における連続一様分布に従うとき、確率密度関数は次のように表します。
における連続一様分布に従うとき、確率密度関数は次のように表します。
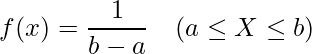
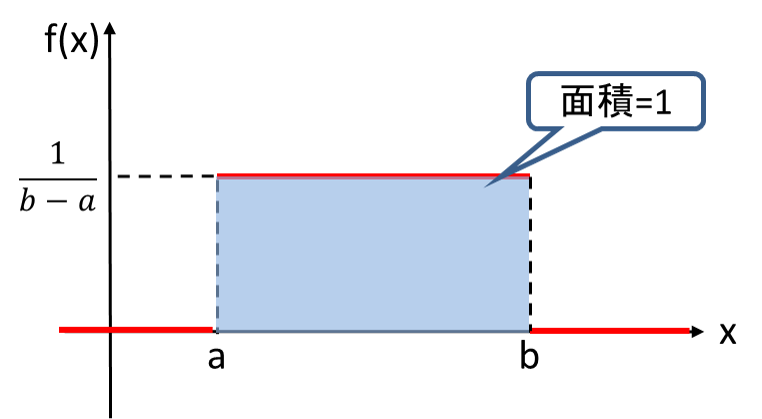
例えば、確率変数![]() が
が![]() における連続一様分布に従うときについて考えてみます。
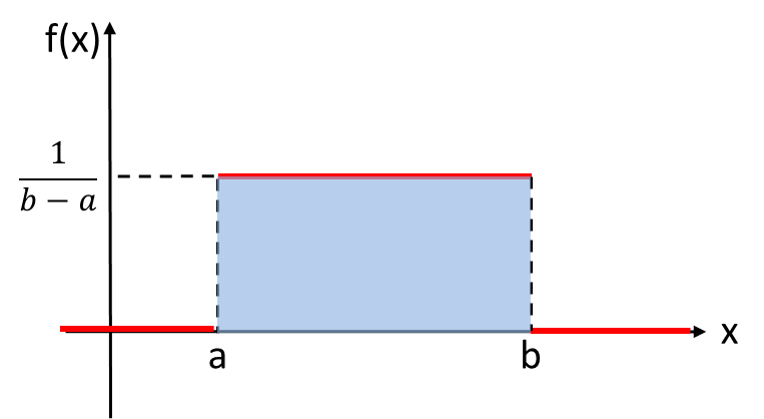
における連続一様分布に従うときについて考えてみます。![]() の範囲では
の範囲では![]() となり、それ以外の範囲では
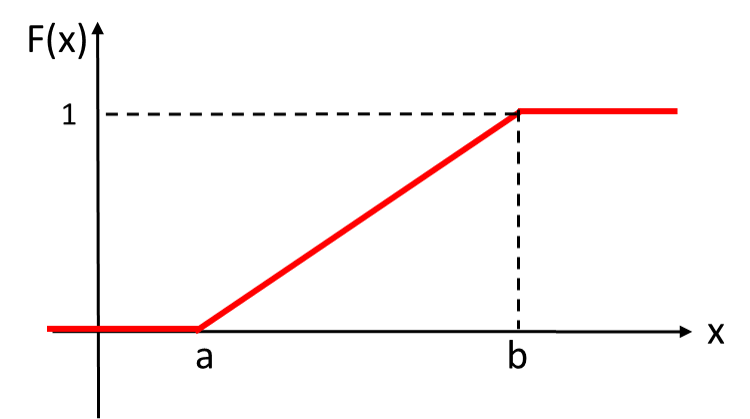
となり、それ以外の範囲では![]() となります。したがって、確率密度関数は次のようなグラフになります。
となります。したがって、確率密度関数は次のようなグラフになります。
![]() が連続型の一様分布
が連続型の一様分布![]() に従っている時、
に従っている時、![]() における期待値
における期待値![]() と分散
と分散![]() は次のようになります。
は次のようになります。
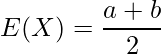
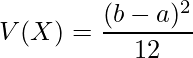
■累積分布関数
確率密度関数![]() が次の式で表される場合の累積分布関数
が次の式で表される場合の累積分布関数![]() を算出してみます。
を算出してみます。
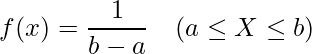
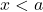 のとき
のとき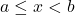 のとき
のとき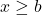 のとき
のとき
![]() では、
では、![]() なので
なので![]() となります。
となります。
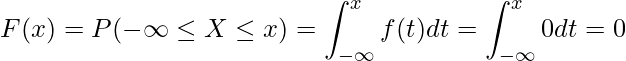
求める範囲は![]() ですが、
ですが、![]() では
では![]() なので
なので![]() となります。したがって、
となります。したがって、![]() の範囲のみを考えればよいことになります。
の範囲のみを考えればよいことになります。
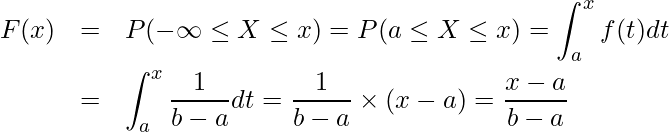
![]() では、
では、![]() なので
なので![]() となります。したがって、
となります。したがって、![]() の範囲のみを考えればよいことになります。
の範囲のみを考えればよいことになります。
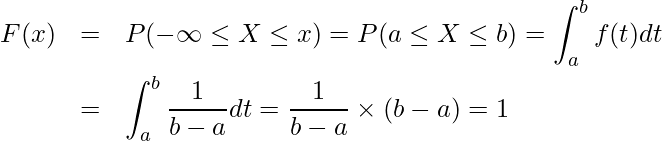
| 確率変数 |
累積分布関数 |
|---|---|
| 0 | |
| 1 |
15. いろいろな確率分布3
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-6. 期待値
- 6. 分散と標準偏差
6-1. 分散
- 12. 累積分布関数と確率変数の期待値・分散
12-1. 累積分布関数とは
- 12. 累積分布関数と確率変数の期待値・分散
12-3. 確率変数の期待値
- 12. 累積分布関数と確率変数の期待値・分散
12-5. 確率変数の分散






