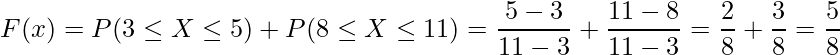BellCurveの統計解析ソフトエクセル統計

15. いろいろな確率分布3

練習問題（15. いろいろな確率分布3）

1

確率変数 $X$ が指数分布 $Ex(4)$ に従うとき、期待値 $E(X)$ を求めよ。

答えを見る

答え閉じる: 指数分布の期待値の公式より、 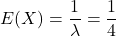$E(X)= \displaystyle \frac{1}{\lambda}=\displaystyle \frac{1}{4}$ と求められます。

2

エクセル統計開発者のKさんのもとには、日々たくさんのお問い合わせメールが届く。お問い合わせメールに対する返信メールの作成時間は1通あたり平均15分の指数分布に従うと仮定できる場合、

作成時間が30分以上となる確率を求めよ。
また、作成時間が5分以上10分以下となる確率を求めよ。

答えを見る

答え閉じる

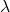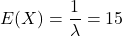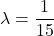まず $\lambda$ を求めます。指数分布の期待値の公式より、 $E(X)= \displaystyle \frac{1}{\lambda}=15$ なので、 $\lambda= \displaystyle \frac{1}{15}$ と求められます。

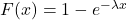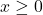1：指数分布の累積分布関数は $F(x)=1-e^{- \lambda x}$ （ただし $x \geq 0$ ）です。求める確率は「メールの作成時間が30分以下となる確率」の余事象です。したがって、次のように計算できます。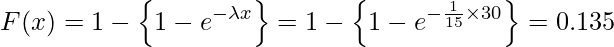

$\displaystyle F(x)=1- \left\{1-e^{- \lambda x} \right\}=1- \left\{1-e^{- \frac{1}{15} \times 30} \right\}=0.135$

2：返信メールの作成時間が5分以下となる確率は次のように求められます。

$\displaystyle F(x)=1-e^{- \lambda x}=1-e^{- \frac{1}{15} \times 5}=0.2835$

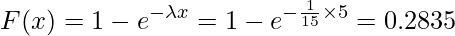
同様に、10分以下となる確率は次のように求められます。

$\displaystyle F(x)=1-e^{- \lambda x}=1-e^{- \frac{1}{15} \times 10}=0.4866$

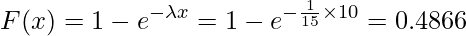
求める確率は5分以上10分以下となる確率です。これは「10分以下となる確率」から「5分以下となる確率」を引いたものです。したがって、 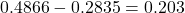$0.4866-0.2835=0.203$ となります。

3

確率変数 $X$ （ $X=1,2,3,4,5,6,7,8$ ）が離散一様分布に従うとき、期待値 $E(X)$ を求めよ。

答えを見る

答え閉じる

離散一様分布の期待値の公式より、

$\displaystyle E(X)= \frac{8+1}{2}= 4.5$

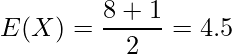
と求められます。なお、離散一様分布はN面のさいころの出目と考えることも出来ます。この問題の場合、8面さいころの出る目の期待値と一致します。

4

確率変数 $X$ （ $X=1,2,3,4,5,6,7,8$ ）が離散一様分布に従うとき、分散 $V(X)$ を求めよ。

答えを見る

答え閉じる

離散一様分布の分散の公式より、

$\displaystyle V(X)= \frac{8^2 -1}{12}= \frac{21}{4}=5.25$

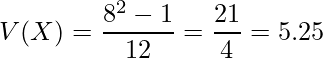
と求められます。

5

3以上11以下の範囲で乱数を10,000個作成したとき、その中で5以下、もしくは8以上の値をとる確率はいくらか。

答えを見る

答え閉じる: 連続一様分布の累積分布関数の公式より、次のように計算できます。

$\displaystyle F(x)=P(3 \leq X \leq 5)+P(8 \leq X \leq 11)= \frac{5-3}{11-3} + \frac{11-8}{11-3} = \frac{2}{8} + \frac{3}{8} = \frac{5}{8}$

次の章へ進む

15. いろいろな確率分布3

統計学やデータ分析を学ぶなら、大人のための統計教室和（なごみ）［業務提携］

オンラインで無料セミナー開催文系のための統計超入門講座

オンラインで学べる集団セミナー統計基礎セミナー（統計検定(R)2級範囲）

【BellCurve監修】統計検定^®2級対策に最適な模擬問題集1～3を各500円（税込）にて販売中！

Kindleストアで配信中

統計検定^®2級模擬問題集1

500円（税込）

統計検定^®2級模擬問題集2

500円（税込）

統計検定^®2級模擬問題集3

500円（税込）