- Step2. 中級編
- 3. 離散型確率分布
3-1. 二項分布
13-1章で、成功確率![]() のベルヌーイ試行を
のベルヌーイ試行を![]() 回行うときにちょうど
回行うときにちょうど![]() 回成功する確率、すなわち
回成功する確率、すなわち![]() となる確率は次の式から計算できることを学びました。
となる確率は次の式から計算できることを学びました。
![]()
この式から二項分布![]() の期待値を求めてみます。
の期待値を求めてみます。
■期待値の算出
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X] &=& \sum^{n}_{i=0} x \times p_i \\ &=& \sum_{x=0}^n x \times {}_{n} \mathrm{C}_{x} p^{x} (1-p)^{n-x} \\ &=& \sum_{x=1}^n x \times n \times \frac{1}{x} \times {}_{n-1} \mathrm{C}_{x-1} p^{x} (1-p)^{n-x} \\ &=& \sum_{x=1}^n n \times {}_{n-1} \mathrm{C}_{x-1} p^{x} (1-p)^{n-x} \\ &=& \sum_{x=1}^n n \times {}_{n-1} \mathrm{C}_{x-1} \times p \times p^{x-1} (1-p)^{n-x} \\ &=& \sum_{x=1}^n np \times {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} \\ &=& np\sum_{x=1}^n {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-1b2c82be7dddc3cdcb905aad30078fb6_l3.png)
ここで、![]() 、
、![]() とおくと
とおくと
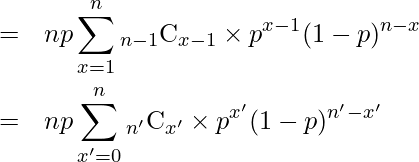
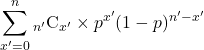 は二項分布の確率の総和であることから「1」になります。したがって、
は二項分布の確率の総和であることから「1」になります。したがって、
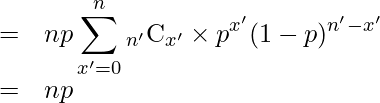
となります。
■分散の算出
分散を求めるには、![]() を使います。まず
を使います。まず![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2] &=& \sum^{n}_{i=1} x^2 \times p_i \\ &=& \sum_{x=0}^n x^2 \times {}_{n} \mathrm{C}_{x} p^{x} (1-p)^{n-x} \\ &=& \sum_{x=1}^n x^2 \times n \times \frac{1}{x} \times {}_{n-1} \mathrm{C}_{x-1} p^{x} (1-p)^{n-x} \\ &=& \sum_{x=1}^n x \times n \times {}_{n-1} \mathrm{C}_{x-1} p^{x} (1-p)^{n-x} \\ &=& \sum_{x=1}^n x \times n \times {}_{n-1} \mathrm{C}_{x-1} \times p \times p^{x-1} (1-p)^{n-x} \\ &=& \sum_{x=1}^n np \times x \times {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} \\ &=& np\sum_{x=1}^n x \times {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} \\ &=& np\sum_{x=1}^n (x-1+1) \times {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} \\ &=& np \left\{ \sum_{x=1}^n (x-1) \times {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} + \sum_{x=1}^n {}_{n-1} \mathrm{C}_{x-1} \times p^{x-1} (1-p)^{n-x} \right\} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-f027741f19d129fc31d2cb3ada335513_l3.png)
ここで、![]() は期待値の算出式から
は期待値の算出式から![]() となります。また、
となります。また、![]() は二項分布の確率の総和であることから「1」になります。したがって、
は二項分布の確率の総和であることから「1」になります。したがって、
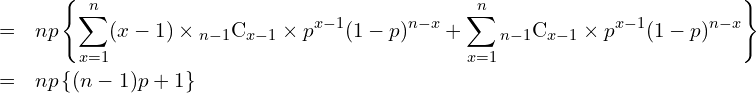
となります。次に![]() を求めます。
を求めます。
これらを使って分散![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& np \left\{ (n-1)p + 1 \right\} - (np)^2 \\ &=& np-np^2 \\ &=& np(1-p) \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-ad70cf237f9c6cecee5d0d161ba8df12_l3.png)
となります。
■モーメント母関数を用いた期待値の算出
2-1章で学んだモーメント母関数を使って期待値を算出してみます。まずはじめに二項分布のモーメント母関数を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M_X(t) &=& E[e^{tX}] \\ &=& \sum_{x}{e^{tx}f(x)} \\ &=& \sum_{x}{e^{tx} \times {}_{n}\mathrm{C}_{x} p^{x} (1-p)^{n-x}} \\ &=& \sum_{x}{{}_{n}\mathrm{C}_{x} e^{tx} p^{x} (1-p)^{n-x}} \\ &=& \sum_{x}{{}_{n}\mathrm{C}_{x} (e^{t}p)^{x} (1-p)^{n-x}} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-bcc7892ace14ba5b6bc756b1a8d06028_l3.png)
二項定理より
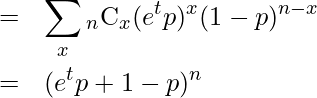
となります。2-1章で学んだように
であることから、まず![]() をtで1回微分します。
をtで1回微分します。
0を代入すると
となります。
■モーメントを用いた分散の算出
2-1章で学んだように
であることから、![]() をtで2回微分します。
をtで2回微分します。
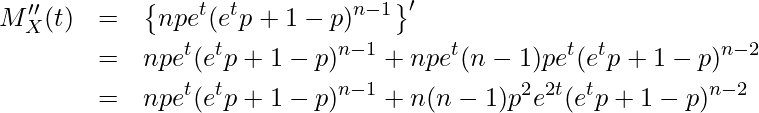
0を代入すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M''_X(0) &=& E[X^2] \\ &=& np(p+1^p)^{n-1} + n(n-1)p^{2}(p+1-p)^{n-2} \\ &=& np+n(n-1)p^{2} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-9f849bf7fb70517e7fe7a4c3b4229dce_l3.png)
となることから、V[X]は次のように計算できます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& np+n(n-1)p^{2}-(np)^2 \\ &=& np+(np)^2-np^2-(np)^2 \\ &=& np-np^2 \\ &=& np(1-p) \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-952f1723d386b1386ce11c94d3e13e1e_l3.png)






