- Step2. 中級編
- 2. 確率分布
2-2. モーメント
モーメント(積率)とは、確率変数![]() の分布について表したものです。12-3章や12-5章で既に学びましたが、確率変数
の分布について表したものです。12-3章や12-5章で既に学びましたが、確率変数![]() の期待値は
の期待値は
であり、分散は
と表すことができます。
■モーメントの定義
これらの式から確率分布の形は次のような式を使って表すことができることが分かります。
このとき、![]() をXの原点まわりのr次のモーメントといいます。また、
をXの原点まわりのr次のモーメントといいます。また、![]() をXの平均値(期待値)まわりのr次のモーメントと言います。
をXの平均値(期待値)まわりのr次のモーメントと言います。
この式を使うと、平均は「原点まわりの1次のモーメント」、分散は「平均値まわりの2次のモーメント」となります。
3-5章で学んだ歪度(skewness)と尖度(kurtosis)はそれぞれ
![Rendered by QuickLaTeX.com \displaystyle skewness = \frac{E[(X-\mu)^3]}{\sigma^3}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-407bb00059816fe6d8a2b89c2faa83af_l3.png)
![Rendered by QuickLaTeX.com \displaystyle kurtosis = \frac{E[(X-\mu)^4]}{\sigma^4}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-8e8e1882773c0f783c635976f63f38b7_l3.png)
で定義されます。これらの式から、歪度は「平均値まわりの3次のモーメント」を![]() で割ったもの、尖度は「平均値まわりの4次のモーメント」を
で割ったもの、尖度は「平均値まわりの4次のモーメント」を![]() で割ったものと言うことができます。
で割ったものと言うことができます。
■モーメント母関数とは
![]() が任意の実数であるとき、確率変数
が任意の実数であるとき、確率変数![]() に対し、
に対し、![]() の
の![]() 乗の期待値
乗の期待値![]() を確率変数
を確率変数![]() のモーメント母関数といい、次の式で定義されます。
のモーメント母関数といい、次の式で定義されます。
・離散型確率変数![]() の場合
の場合
![Rendered by QuickLaTeX.com \displaystyle M_X(t) = E[e^{tX}] = \sum_{x}{e^{tx}f(x)}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-1d43502d11a8c8da155b8be4d4f1744e_l3.png)
・連続型確率変数![]() の場合
の場合
![Rendered by QuickLaTeX.com \displaystyle M_X(t) = E[e^{tX}] = \int_{-\infty}^{\infty}{e^{tx}f(x)dx}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-f325e8e1891fa2f9aa4b2655265c9c9f_l3.png)
となります。ただし、tによってはモーメント母関数が存在しない場合もあります。
■モーメント母関数の使い方
モーメント母関数の良い点は、この1つの関数からすべての次数のモーメントを生成することができる点です。![]() をマクローリン展開すると次のようになります。
をマクローリン展開すると次のようになります。
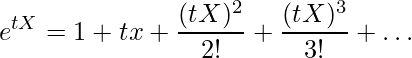
したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M_X(t) &=& E[e^{tX}] \\ &=& E \left[1 + tX + \frac{(tX)^2}{2!} + \frac{(tX)^3}{3!} + \dots \right] \\ &=& E[1] + tE[X] + \frac{t^2E[X^2]}{2!} + \frac{t^3E[X^3]}{3!} + \dots \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7df65d0ede02f7e6eb9af3d551a16ba3_l3.png)
となります。この式をtで1回微分をすると
![Rendered by QuickLaTeX.com \displaystyle M'_X(t) = \frac{d}{dt} E[e^{tX}] = E[X] + tE[X^2] + \frac{1}{2!}t^2E[X^3] + \dots](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-cffb1feb2dcc2381c5f5860db4d0fc7b_l3.png)
となり、2回微分をすると
![Rendered by QuickLaTeX.com \displaystyle M''_X(t) = \frac{d}{dt} E[e^{tX}] = E[X^2] + tE[X^3] + \dots](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-900313cd76b86ff5cabf8a63781b4b91_l3.png)
となります。これらの式に![]() を代入すると、次の式が導出されます。
を代入すると、次の式が導出されます。
つまり、モーメント母関数をr回微分して0を代入することでr次のモーメントを求めることができます。これらのモーメントと、12-5章で学んだ
を組み合わせることで、様々な確率分布の期待値や分散を簡単に求めることができます。







