- Step2. 中級編
- 3. 離散型確率分布
3-4. 多項分布
■多項分布
事象 ![]() が起きる確率をそれぞれ
が起きる確率をそれぞれ ![]() とします。確率変数
とします。確率変数 ![]() が多項分布に従う場合、それぞれの試行が
が多項分布に従う場合、それぞれの試行が ![]() 回起こる確率は次の式から計算できます。
回起こる確率は次の式から計算できます。
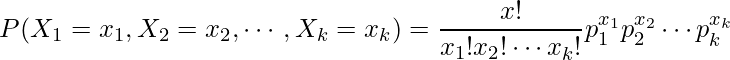
![]() の場合を考えてみます。このとき、
の場合を考えてみます。このとき、
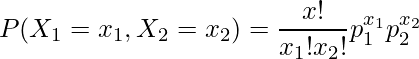
となります。ただし、![]() 、
、![]() であることから、この式は次のように書き換えられます。
であることから、この式は次のように書き換えられます。
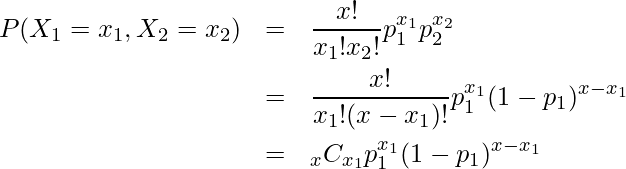
この式は、成功確率が ![]() のベルヌーイ試行を
のベルヌーイ試行を ![]() 回行うときに成功する回数
回行うときに成功する回数 ![]() が従う確率分布である「二項分布」を表しています。すなわち、
が従う確率分布である「二項分布」を表しています。すなわち、![]() における多項分布の確率分布は二項分布と一致します。
における多項分布の確率分布は二項分布と一致します。
例題:
あるゲームセンターにおいてあるじゃんけんマシーンは、「グー」「チョキ」「パー」がそれぞれ「20%」「30%」「50%」の確率で出ます。グー、チョキ、パーそれぞれが出る回数 ![]() が多項分布分布に従うとすると、このじゃんけんマシーンで5回遊んだ場合に「グー」が2回、「チョキ」が2回、「パー」が1回出る確率はいくらでしょうか。
が多項分布分布に従うとすると、このじゃんけんマシーンで5回遊んだ場合に「グー」が2回、「チョキ」が2回、「パー」が1回出る確率はいくらでしょうか。
グーが出る事象を ![]() 、チョキが出る事象を
、チョキが出る事象を ![]() 、パーが出る事象を
、パーが出る事象を ![]() とします。このときそれぞれの事象
とします。このときそれぞれの事象 ![]() が起きる確率とその回数は
が起きる確率とその回数は ![]() となります。したがって、求める確率は
となります。したがって、求める確率は
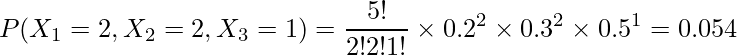
となります。
■期待値の算出
多項分布の期待値を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X_i] &=& \sum^{k}_{x_i=1} x_i \times \frac{x!}{x_1!x_2! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} x_i \times \frac{x!}{x_1!x_2! \cdots x_i! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} x_i \times \frac{x!}{x_1!x_2! \cdots (x_i-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} \frac{x!}{x_1!x_2! \cdots (x_i-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_i}_i \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} \frac{x(x-1)!}{x_1!x_2! \cdots (x_i-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p_ip^{x_i-1}_i \cdots p^{x_k}_k \\ &=& xp_i \times \sum^{k}_{x_i=1} \frac{(x-1)!}{x_1!x_2! \cdots (x_i-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_i-1}_i \cdots p^{x_k}_k \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-e05f754190405af897c62dd80866cd9b_l3.png)
ここで、![]() は多項分布の確率質量関数を表します。したがって、
は多項分布の確率質量関数を表します。したがって、
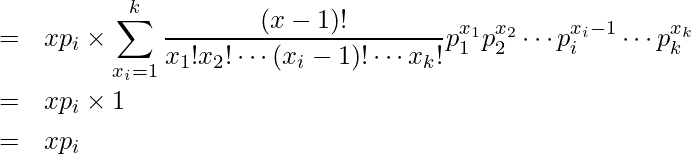
となります。
■分散の算出
分散を求めるには、![]() を使います。まず多項式における
を使います。まず多項式における![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2_i] &=& \sum^{k}_{x_i=1} x^2_i \times \frac{x!}{x_1!x_2! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} \{x_i(x_i-1)+x_i\} \times \frac{x!}{x_1!x_2! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} x_i(x_i-1) \times \frac{x!}{x_1!x_2! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k + \sum^{k}_{x_i=1} x_i \times \frac{x!}{x_1!x_2! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{x_i=1} \frac{x!}{x_1!x_2! \cdots (x_i-2) \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k + xp_i \\ &=& \sum^{k}_{x_i=1} \frac{x(x-1)(x-2)!}{x_1!x_2! \cdots (x_i-2) \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{2}_{i} p^{x_{i}-2}_{i} \cdots p^{x_k}_k + xp_i \\ &=& x(x-1)p^{2}_{i} \sum^{k}_{x_i=1} \frac{(x-2)!}{x_1!x_2! \cdots (x_i-2) \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_{i}-2}_{i} \cdots p^{x_k}_k + xp_i \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-e92c302dc4c6a9ca17211e7039d69b98_l3.png)
ここで、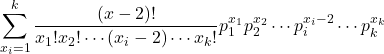 は多項分布の確率質量関数を表します。したがって、
は多項分布の確率質量関数を表します。したがって、
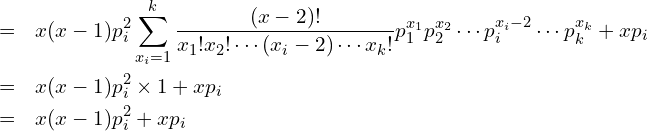
となります。次に![]() を求めます。
を求めます。
これらを使って分散![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& x(x-1)p^{2}_{i} + xp_i - x^2p^2_i \\ &=& x^2p^{2}_{i} -xp^{2}_{i} + xp_i - x^2p^2_i \\ &=& -xp^{2}_{i} + xp_i \\ &=& xp_i(1-p_{i}) \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-f7c6cd6eeb876d974277efda0ffc3a12_l3.png)
となります。
■共分散の算出
![]() と
と![]() の共分散を求めるには、
の共分散を求めるには、![]() を使います。まず多項式における
を使います。まず多項式における![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X_i X_j] &=& \sum^{n}_{x_i=1} x_i x_j \times \frac{x!}{x_1!x_2! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{} x_i x_j \times \frac{x!}{x_1!x_2! \cdots x_i!x_j! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{} x_i x_j \times \frac{x!}{x_1!x_2! \cdots (x_i-1)!(x_j-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_k}_k \\ &=& \sum^{k}_{} \frac{x!}{x_1!x_2! \cdots (x_i-1)!(x_j-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_i}_i \cdots p^{x_k}_k \\ &=& \sum^{k}_{} \frac{x(x-1)(x-2)!}{x_1!x_2! \cdots (x_i-1)!(x_j-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p_ip^{x_i-1}_i p_jp^{x_j-1}_j \cdots p^{x_k}_k \\ &=& x(x-1)p_i p_j \times \sum^{k}_{} \frac{(x-2)!}{x_1!x_2! \cdots (x_i-1)!(x_j-1)! \cdots x_k!} p^{x_1}_1 p^{x_2}_2 \cdots p^{x_i-1}_i p^{x_j-1}_j \cdots p^{x_k}_k \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-0b5f7ad079e5418c8f882e3da227d247_l3.png)
ここで、![]() は多項分布の確率質量関数を表します。したがって、
は多項分布の確率質量関数を表します。したがって、
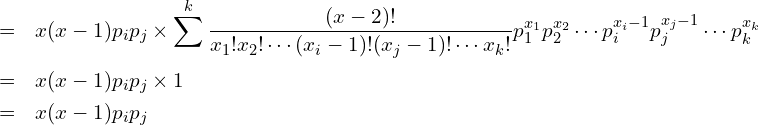
これを使って共分散![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle Cov[X_i, X_j] &=& E[X_i X_j] - E[X_i]E[X_j] \\ &=& x(x-1)p_i p_j - xp_i xp_j \\ &=& x^2 p_i p_j - x p_i p_j - x^2p_i p_j \\ &=& - x p_i p_j \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-1fc6d117f5b60a6daddef9a978953fcd_l3.png)
となります。






