- Step2. 中級編
- 3. 離散型確率分布
3-3. 幾何分布
成功確率が![]() である独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数
である独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数![]() が従う確率分布を幾何分布といいます。確率変数が幾何分布に従う場合、成功確率が
が従う確率分布を幾何分布といいます。確率変数が幾何分布に従う場合、成功確率が![]() の試行において、
の試行において、![]() 回目で初めて成功する確率は次の式から計算できます。
回目で初めて成功する確率は次の式から計算できます。
![]()
この式から幾何分布![]() の期待値を求めてみます。
の期待値を求めてみます。
■期待値の算出
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X] &=& \sum^{n}_{x=1} x \times p_x \\ &=& \sum_{x=1}^n x \times (1-p)^{x-1} p \\ &=& p \sum_{x=1}^n x \times (1-p)^{x-1} \\ &=& p \left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 3 \times (1-p)^{2} + \dots \right\} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-5ba2eab65157ec6d6116b18688b8f666_l3.png)
となります。ここで、![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle (1-p)E[X] &=& p (1-p)\left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 3 \times (1-p)^{2} + \dots \right\} \\ &=& p \left\{ 1 \times (1-p)^{1} + 2 \times (1-p)^{2} + 3 \times (1-p)^{3} + \dots \right\} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-858b773c6bbd77edff764687abc6b2fa_l3.png)
となります。![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X]-(1-p)E[X] &=& pE[X] \\ &=& p \left\{ (1-p)^{0} + (1-p)^{1} + (1-p)^{2} + (1-p)^{3} + \dots \right\} \\ &=& p \sum_{x=0}^n (1-p)^{x} \\ E[X] &=& \sum_{x=0}^n (1-p)^{x} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-0ceacf51cd3f2084432463b272e69933_l3.png)
となることから、等比数列の和の公式より
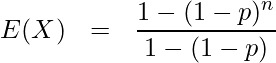
ここで![]() を考えると
を考えると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X] &=& \lim_{n \to \infty} \frac{1-(1-p)^n}{1-(1-p)} \\ &=& \frac{1}{p} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-3f4662af922e0c94f8534c09abb72dcf_l3.png)
となります。
■分散の算出
分散を求めるには、![]() を使います。まず
を使います。まず![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2] &=& \sum^{n}_{x=1} x^2 \times p_x \\ &=& \sum_{x=1}^n x^2 \times (1-p)^{x-1} p \\ &=& p \sum_{x=1}^n x^2 \times (1-p)^{x-1} \\ &=& p \left\{ 1^2 \times (1-p)^{0} + 2^2 \times (1-p)^{1} + 3^2 \times (1-p)^{2} + \dots \right\} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-a4f839e8667c2eebd09be886572d8502_l3.png)
となります。ここで、![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle (1-p)E[X^2] &=& p (1-p)\left\{ 1^2 \times (1-p)^{0} + 2^2 \times (1-p)^{1} + 3^2 \times (1-p)^{2} + \dots \right\} \\ &=& p \left\{ 1^2 \times (1-p)^{1} + 2^2 \times (1-p)^{2} + 3^2 \times (1-p)^{3} + \dots \right\} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-5bbecb4b8a2d77b442e88d41d8690061_l3.png)
となります。![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2]-(1-p)E[X^2] &=& pE[X^2] \\ &=& p \left\{ 1^2 \times (1-p)^{0} + (2^2-1^2) \times (1-p)^{1} + (3^2-2^2) \times (1-p)^{2} + \dots \right\} \\ &=& p \left\{ 1 \times (1-p)^{0} + 3 \times (1-p)^{1} + 5 \times (1-p)^{2} + \dots \right\} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-d8416753ae274a5f6138b2ddf3da224d_l3.png)
この式を整理すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2] &=& \sum_{x=0}^n (2x+1)(1-p)^{x} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-8fc3b226d906b2be18f5ed664a18e188_l3.png)
となります。この式をよく見ると、等差数列と等比数列の積になっています。公比![]() をかけた式を作り、
をかけた式を作り、![]() を計算します。
を計算します。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2]-(1-p)E[X^2] &=& pE[X^2] \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - (1-p)\sum_{x=0}^n (2x+1)(1-p)^{x} \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - \sum_{x=0}^n (2x+1)(1-p)^{x+1} \\ &=& \left\{ 1 \times (1-p)^{0} + 3 \times (1-p)^{1} + 5 \times (1-p)^{2} + \dots \right\} \\ && - \left\{ 1 \times (1-p)^{1} + 3 \times (1-p)^{2} + 5 \times (1-p)^{3} + \dots \right\} \\ &=& \left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 2 \times (1-p)^{2} + \dots \right\} \\ &=& 1 + 2 \times \sum_{x=1}^n (1-p)^{x} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b2d2c0976064248e6fc602162895e947_l3.png)
となります。等比数列の和の公式を利用すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle pE[X^2] &=& 1 + 2(1-p) \times \frac{1-(1-p)^n}{1-(1-p)} \\ &=& \frac{p+\{2(1-p)\}\{1-(1-p)^n\}}{p} \\ E[X^2] &=& \frac{p+\{2(1-p)\}\{1-(1-p)^n\}}{p^2} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-bfcf3298c4c965348cbd6f2dc32aaa93_l3.png)
ここで![]() を考えると
を考えると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2] &=& \lim_{n \to \infty} \frac{p+\{2(1-p)\}\{1-(1-p)^n\}}{p^2} \\ &=& \frac{p+\{2(1-p)\}}{p^2} \\ &=& \frac{2-p}{p^2} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-d68284d125c0ca15117b2ce0a4763844_l3.png)
となります。次に![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \displaystyle \left\{E[X] \right\}^2 = \frac{1}{p^2}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b1a25058fe3a408f063e21e688e3c3e8_l3.png)
これらを使って分散![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& \frac{2-p}{p^2} - \frac{1}{p^2} \\ &=& \frac{1-p}{p^2} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-166dbb58b27e9a17ebf094778d550134_l3.png)
となります。
■モーメント母関数を用いた期待値の算出
2-1章で学んだモーメント母関数を使って期待値を算出してみます。まずはじめに幾何分布のモーメント母関数を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M_X(t) &=& E[e^{tX}] \\ &=& \sum_{x}{e^{tx}f(x)} \\ &=& \sum_{x}{e^{tx} \times (1-p)^{x-1} p} \\ &=& \frac{p}{1-p}\sum_{x}{e^{tx} \times (1-p)^{x}} \\ &=& \frac{p}{1-p}\sum_{x} {\{e^{t}(1-p)\}^{x}} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-083be6b1ca78f0b16599141c6eecd7f5_l3.png)
となることから、等比数列の和の公式より
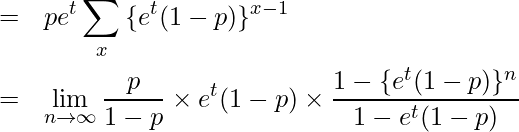
この式は![]() のときに収束します。このとき、
のときに収束します。このとき、
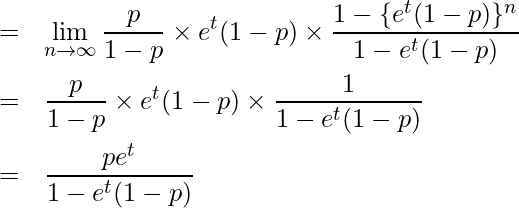
となります。2-1章で学んだように
であることから、まず![]() をtで1回微分します。
をtで1回微分します。
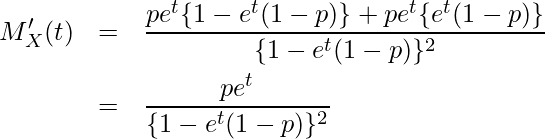
t=0を代入すると
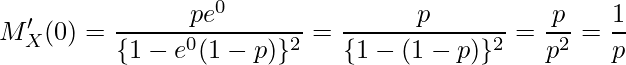
となります。
■モーメントを用いた分散の算出
2-1章で学んだように
であることから、![]() をtで2回微分します。
をtで2回微分します。
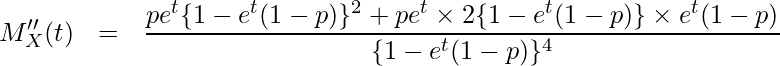
t=0を代入すると
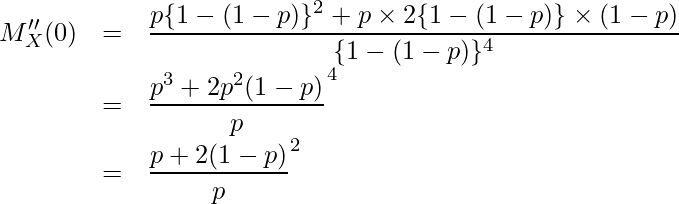
となることから、V[X]は次のように計算できます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] = E[X^2] - \{E[X]\}^2 = \frac{p+2(1-p)}{p}^2} - \frac{1}{p^2} = \frac{1-p}{p^2} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-09b809f249b8bf65f14c9183a702a041_l3.png)







