- Step1. 基礎編
- 20. 母平均の区間推定(母分散未知)
20-1. 標本とt分布
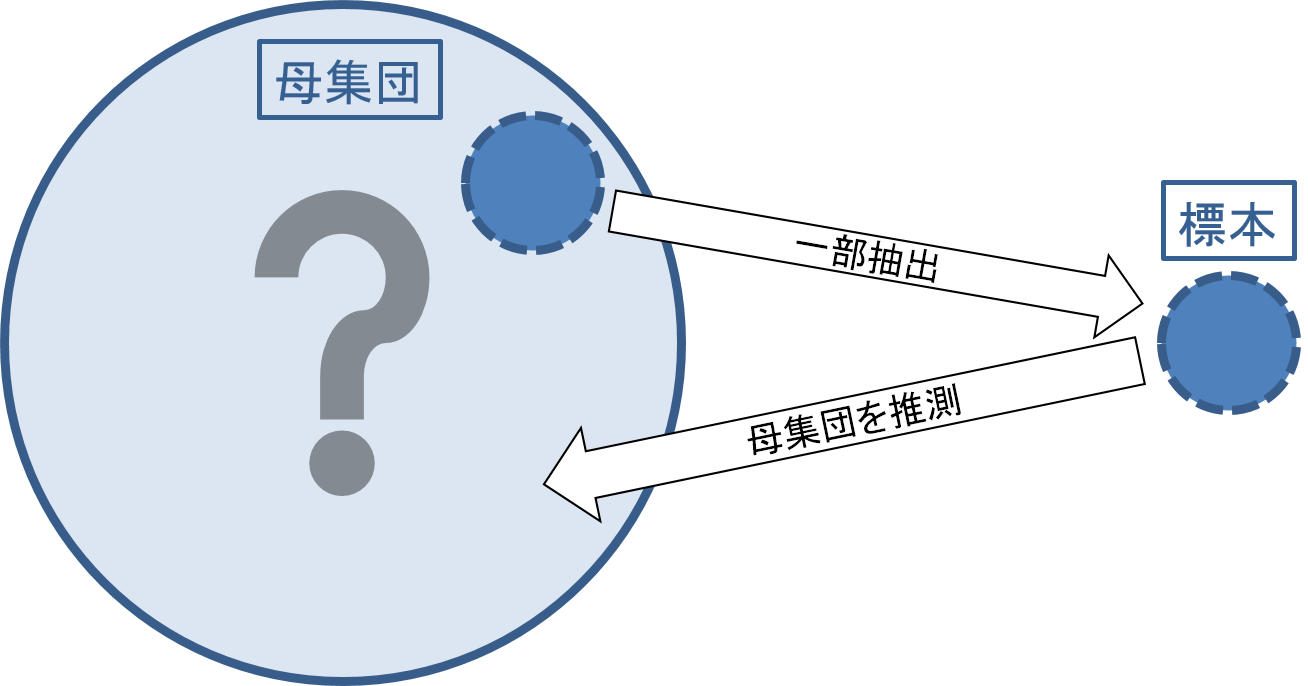
20章では、母分散が分からない場合の母平均の区間推定について説明します。19章では母分散が分かっている場合の母平均の信頼区間の算出方法について学びましたが、母平均が分からないのに母分散だけは分かっているという状況は現実にはほとんどありません。したがって、通常母平均の区間推定を行う場合にはこの章で説明するt分布(あるいはStudentのt分布ともいいます)を用いた方法が使われます。
まず、ここまでの章で学んだ統計量の記号を次の表にまとめます。母分散を表す![]() と不偏分散を表す
と不偏分散を表す![]() は、今後もよく出てくるので覚えておくと便利です。
は、今後もよく出てくるので覚えておくと便利です。
| 統計量で用いられる記号 | 母集団 | 標本 |
|---|---|---|
| 平均 | μ | |
| 分散 |
母分散が分からない場合、母分散![]() を使うことはできません。つまり、19-2章で学習した母平均の95%信頼区間を求める式は使えません。
を使うことはできません。つまり、19-2章で学習した母平均の95%信頼区間を求める式は使えません。
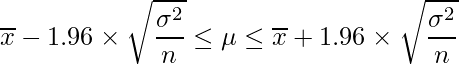
そのため、母分散![]() の代わりに不偏分散
の代わりに不偏分散![]() を使います。
を使います。![]() を使って母平均の区間推定を行う場合には、標準正規分布ではなく「t分布」を使います。
を使って母平均の区間推定を行う場合には、標準正規分布ではなく「t分布」を使います。
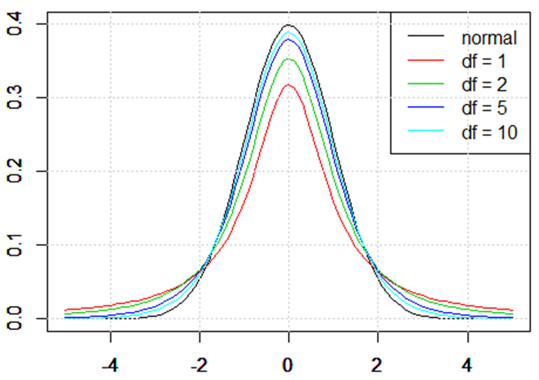
t分布は標準正規分布とよく似た形の分布で、パラメータである「自由度」によって分布の形が変わるという特徴を持っています。自由度を変化させた時のt分布の形を見てみます。次のグラフは自由度(グラフ中ではdfで表示しています)が1, 2, 5, 10である場合のt分布(赤、緑、青、水色線)と標準正規分布(黒線:normal)を表したものです。自由度が大きくなるにつれて、標準正規分布に近づくことが分かります。
平均![]() 、不偏分散
、不偏分散![]() の正規分布に従う母集団から抽出したサンプルサイズnの標本を使って算出される次に示す統計量tの値は、自由度
の正規分布に従う母集団から抽出したサンプルサイズnの標本を使って算出される次に示す統計量tの値は、自由度![]() のt分布に従います。したがって、母分散が分からない場合にはt分布を使って区間推定を行うことができるのです。
のt分布に従います。したがって、母分散が分からない場合にはt分布を使って区間推定を行うことができるのです。
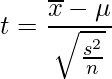
■t分布の性質
- t分布の成り立ち
標準正規分布N(0, 1)に従うZと自由度nのカイ二乗分布Wがあり、これらが互いに独立であるとき、次の式から算出されるtは自由度nのt分布に従います。
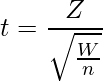
ここで、正規分布
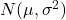 に従う母集団から抽出したサンプルサイズnの標本
に従う母集団から抽出したサンプルサイズnの標本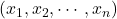 を考えます。定義より、
を考えます。定義より、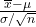 は標準正規分布N(0, 1)に、
は標準正規分布N(0, 1)に、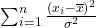 は自由度(n-1)のカイ二乗分布に従います。これらを自由度(n-1)としたときの上式に代入すると、
は自由度(n-1)のカイ二乗分布に従います。これらを自由度(n-1)としたときの上式に代入すると、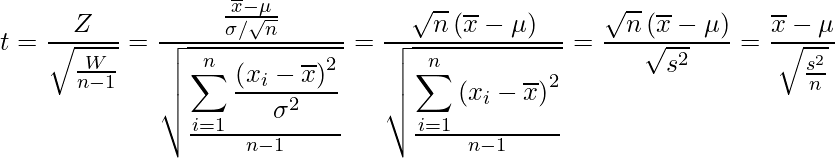
となります。
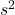 は不偏分散を表します。したがって、この式から算出されるtは自由度(n-1)のt分布に従います。
は不偏分散を表します。したがって、この式から算出されるtは自由度(n-1)のt分布に従います。 - 期待値と分散
確率変数
 が自由度
が自由度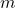 のt分布に従っている時、
のt分布に従っている時、 の期待値
の期待値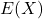 と分散
と分散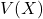 は次のようになります。
は次のようになります。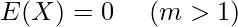
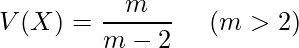
【コラム】t分布の発見
t分布はゴセット(William Sealy Gosset)によって初めて示されました。ゴセットはギネスビールの社員だったことから、t分布についての論文を発表する際に「Student」というペンネームを用いました。ゴセットがどのようにしてt分布を発見したかについては、「統計学を拓いた異才たち」に詳しく書かれています。この本、とても面白いのでおすすめです。
20. 母平均の区間推定(母分散未知)
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 18. 母平均の点推定
18-4. 標本分散と不偏分散
- 19. 母平均の区間推定(母分散既知)
19-2. 母平均の信頼区間の求め方(母分散既知)
- ブログ
ゴセット、フィッシャー、ネイマン








