- Step1. 基礎編
- 18. 母平均の点推定
18-4. 標本分散と不偏分散
母平均の点推定を行うと、「不偏分散」が出力されます。6-1章で既に学んだ分散(標本分散)とのちがいに触れながら不偏分散について説明します。
なお、統計学の時間では母分散を ![]() 、標本分散を
、標本分散を ![]() 、不偏分散を
、不偏分散を ![]() と表します。
と表します。
■標本分散
得られたデータの平均を ![]() 、個々のデータを
、個々のデータを![]() 、サンプルサイズをnとすると、標本分散
、サンプルサイズをnとすると、標本分散![]() は、次の式から求められます。
は、次の式から求められます。
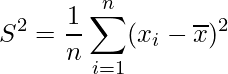
ただし、標本分散は一致推定量ではあるものの不偏推定量ではありません。つまり、nが十分に大きくない場合には標本分散の期待値は母分散に一致せず、母分散より小さくなります。
■不偏分散
標本分散にかわり、標本分散の期待値が母分散に一致するように標本分散の算出式にn/(n-1)をかけたものが不偏分散の算出式となります。したがって、不偏分散は一致性と不偏性をもつ推定量です。不偏分散は一般的に![]() と書き、次の式から算出します。
と書き、次の式から算出します。
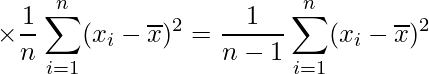
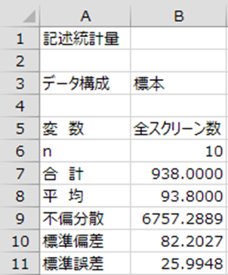
無作為に抽出された10都道府県の合計スクリーン数のデータから不偏分散を求めてみます。
| No. | 都道府県 | 全スクリーン数 |
|---|---|---|
| 1 | 兵庫 | 126 |
| 2 | 大阪 | 224 |
| 3 | 奈良 | 34 |
| 4 | 岩手 | 25 |
| 5 | 千葉 | 199 |
| 6 | 茨城 | 89 |
| 7 | 福岡 | 178 |
| 8 | 山梨 | 14 |
| 9 | 滋賀 | 38 |
| 10 | 鳥取 | 11 |
不偏分散の式にあてはめると
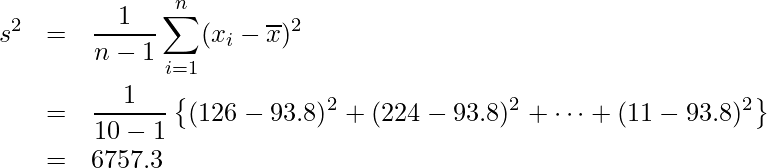
となります。
■おすすめ書籍
子供向けかなーと思いきや、多変量解析やベイズ統計学まで網羅している本格的な”図鑑”でした。結構厚いし読み応えあります。
18. 母平均の点推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 6. 分散と標準偏差
6-1. 分散
- ブログ
標準誤差
- ブログ
不偏分散の平方根は標準偏差の不偏推定量か








