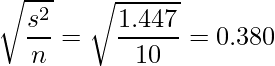- 18. 母平均の点推定
練習問題(18. 母平均の点推定)
1
![]() である場合に母平均
である場合に母平均![]() を推定したい。標本平均
を推定したい。標本平均![]() により
により![]() を推定する場合、25人の平均と100人の平均ではどちらが推定の精度がよいと考えられるか。
を推定する場合、25人の平均と100人の平均ではどちらが推定の精度がよいと考えられるか。

答えを見る
- 答え
 閉じる
閉じる -
標本平均
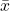 の従う分布は、次のようになります。
の従う分布は、次のようになります。- 25人の平均の場合
- 100人の平均の場合
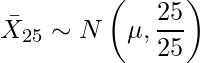
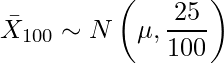
25人の平均では標本平均の標準誤差は
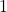 ですが、100人の平均だと標準誤差は
ですが、100人の平均だと標準誤差は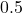 となり、後者の標準誤差の方が小さくなります。したがって、「100人の平均の方が精度が良い」が答えとなります。
となり、後者の標準誤差の方が小さくなります。したがって、「100人の平均の方が精度が良い」が答えとなります。
母平均の推定において、サンプルサイズは大きい方が真の母平均
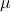 に対してばらつきの少ない推定ができます。
に対してばらつきの少ない推定ができます。
2
不偏分散について述べられた次の文章のうち、誤っているものを選べ。
- 不偏分散は母分散の不偏推定量である
- 一般に、不偏分散の平方根を取ったものは、標準偏差の不偏推定量になる
- 同じデータから標本分散と不偏分散を計算すると、不偏分散の方が常に大きくなる

答えを見る
- 答え
 閉じる
閉じる -
- 正しいです。不偏分散は、母分散の不偏推定量です。
- 誤りです。不偏分散の平方根を取ったものは、標準偏差の不偏推定量とはなりません。(解説)
- 正しいです。標本分散と不偏分散をそれぞれ
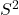 、
、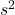 とすると、次の関係が成り立ちます。すなわち、不偏分散は常に標本分散の
とすると、次の関係が成り立ちます。すなわち、不偏分散は常に標本分散の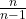 倍となり、
倍となり、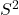 よりも大きな数値になります。また、
よりも大きな数値になります。また、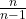 はnが大きくなるほどに1に近づくため、サンプルサイズが大きくなるにつれては標本分散と不偏分散の値は近くなっていくことも分かります。
はnが大きくなるほどに1に近づくため、サンプルサイズが大きくなるにつれては標本分散と不偏分散の値は近くなっていくことも分かります。
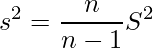
3
推定量の性質について、サンプルサイズに影響される性質は「一致性」と「不偏性」のどちらであるか。

答えを見る
- 答え
 閉じる
閉じる -
答えは「一致性」です。一致性は「サンプルサイズが非常に大きくなれば、推定値が真の値からずれてしまう確率は0に近づく」という性質です。
一方で不偏性は、「推定量の期待値は真の値になる」ことであり「推定値が平均して過小推定でも過大推定でもない」ことを意味します。これは、サンプルサイズとは特に関係ない性質です。
4
ある中学校の1年生300人からランダムに選んだ10人の英語のテストの点数は次のとおりである。この結果から、学年全体の平均点と分散を求めよ。
データ:80 75 40 100 95 55 80 85 70 65

答えを見る
- 答え
 閉じる
閉じる -
10人の平均は74.5です。母集団(学年全体)の平均点を
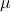 とすると、
とすると、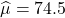 となります。
となります。
母集団から抽出した標本のデータを用いて分散を求めるので、求める分散は不偏分散です。不偏分散は次のように求めます。母分散を
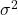 とすると、
とすると、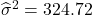 となります。
となります。
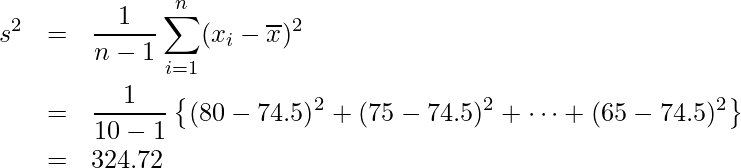
5
ある中学校の1年生300人からランダムに選んだ10人の50m走のタイムは次のとおりである。この結果から、学年全体の平均タイムと標準誤差を求めよ。
データ:7.0 6.2 8.3 10.0 9.1 6.8 7.4 8.5 9.2 7.9

答えを見る
- 答え
 閉じる
閉じる -
10人の平均は8.04です。母集団(学年全体)の平均点を
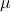 とすると、
とすると、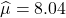 となります。
となります。
不偏分散
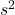 を計算すると1.447になります。標準誤差は不偏分散を用いて次のように求められます。
を計算すると1.447になります。標準誤差は不偏分散を用いて次のように求められます。