19-1. 区間推定とは

区間推定は、母集団の従う分布が正規分布であると仮定できるときに、標本から得られた値を使ってある区間でもって母平均などの母数を推定する方法です。このときの区間のことを「信頼区間」といいます。論文などでは略語表記として「CI」が用いられます。

母平均の区間推定では、母分散が分かっている場合と分からない場合とで、その算出方法が異なります。19章では、母分散が分かっている場合の信頼区間の求め方について説明します。

：母分散 $\sigma^{2}$ の値を使い、標準正規分布を用いて信頼区間を算出する

：次の式から算出される不偏分散 $s^{2}$ の値を使い、t分布を用いて信頼区間を算出する（20章で説明します）

$\displaystyle s^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}$

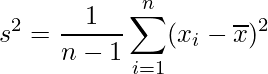
ただし、母平均が分からないのに母分散だけは分かっている、という状況は現実にはほとんどありません。したがって、通常母平均の区間推定を行う場合にはt分布を用いた方法が使われます。

母平均の区間推定では「95%信頼区間（95％CI）」を求めることが多いですが、これは「母集団から標本を取ってきて、その標本平均から母平均の95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」ということを意味します。

また、95％信頼区間以外に「99%信頼区間」や「90%信頼区間」といった区間を求めることもあります。この95％や99%、90%のような、ある区間に母数が含まれる確率のことを「信頼係数」あるいは「信頼度」といいます。

■おすすめ書籍

こちらも、統計学基礎を学ぶ王道本の1つだと思います。初心者にはやや難しい部分もあるかもしれませんが、練習問題を解きながら何度も読み直していくと段々と統計学の考え方が身についていくと思います。