- Step1. 基礎編
- 19. 母平均の区間推定(母分散既知)
19-2. 母平均の信頼区間の求め方(母分散既知)
2015年12月末時点の各都道府県内にある映画館のスクリーンの合計数の区間推定を行ってみます。47都道府県全てのデータを調べるのは面倒なので、無作為に10都道府県のデータを抽出しました。次の表が抽出したデータです。ただし、母分散(47都道府県にある映画館の合計スクリーン数の分散)は![]() =5560であることが分かっており、スクリーン数の分布は正規分布に従うものとします。このデータから「母平均の95%信頼区間」を求めてみます。
=5560であることが分かっており、スクリーン数の分布は正規分布に従うものとします。このデータから「母平均の95%信頼区間」を求めてみます。
| No. | 都道府県 | 全スクリーン数 |
|---|---|---|
| 1 | 兵庫 | 126 |
| 2 | 大阪 | 224 |
| 3 | 奈良 | 34 |
| 4 | 岩手 | 25 |
| 5 | 千葉 | 199 |
| 6 | 茨城 | 89 |
| 7 | 福岡 | 178 |
| 8 | 山梨 | 14 |
| 9 | 滋賀 | 38 |
| 10 | 鳥取 | 11 |
母平均の信頼区間は次の1~4に従って算出します。
- 標本平均
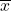 を求める
を求める - 標本平均の標準化を行う
- 2で標準化した値が標準正規分布の95%の面積(=確率)の範囲にあればよい(=両端の2.5%の面積の部分の極端な範囲に入らなければよい)ので、標準正規分布表から上側2.5%点を調べる
- 95%信頼区間を求める
これは抽出した標本の平均値を求めるだけです。この例題の場合、 ![]() =93.8となります。
=93.8となります。
母平均を![]() 、母分散を
、母分散を![]() 、抽出したサンプルサイズをnとすると、次の式から標本平均を標準化できます。
、抽出したサンプルサイズをnとすると、次の式から標本平均を標準化できます。
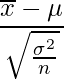
中心極限定理は、平均![]() 、分散
、分散![]() に従う母集団からサンプルサイズnの標本を抽出する時、その平均値
に従う母集団からサンプルサイズnの標本を抽出する時、その平均値![]() の分布はnが大きくなるにつれて正規分布
の分布はnが大きくなるにつれて正規分布![]() に近づくというものであることは、17‐4章で既に学びました。母平均の信頼区間の算出にはこの中心極限定理を利用します。標本平均を標準化する理由は、標準正規分布を利用するためです。
に近づくというものであることは、17‐4章で既に学びました。母平均の信頼区間の算出にはこの中心極限定理を利用します。標本平均を標準化する理由は、標準正規分布を利用するためです。
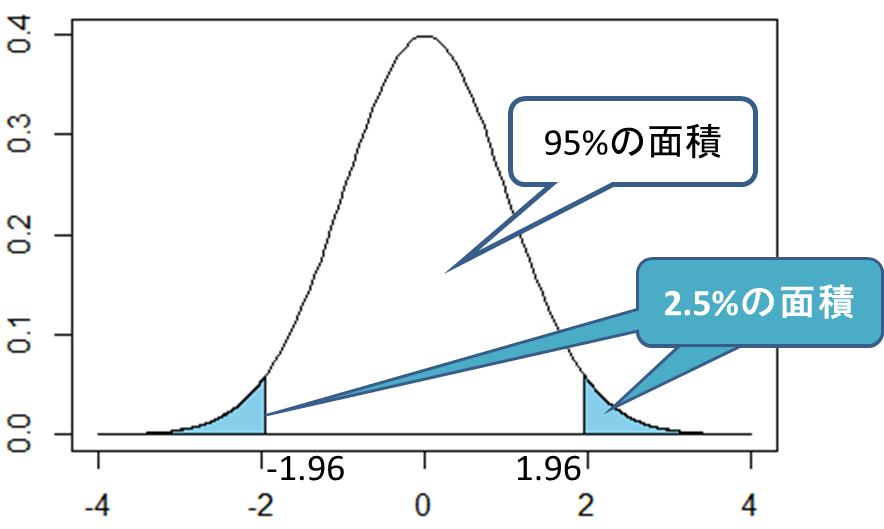
標準正規分布において、ある値より大きな値をとる確率が2.5%となるとき、このある値のことを「上側2.5%点」といいます。標準正規分布表(次表)から、上側2.5%点となる値(z)を探します。
| .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.500 | 0.496 | 0.492 | 0.488 | 0.484 | 0.480 | 0.476 | 0.472 | 0.468 | 0.464 |
| 0.1 | 0.460 | 0.456 | 0.452 | 0.448 | 0.444 | 0.440 | 0.436 | 0.433 | 0.429 | 0.425 |
| 0.2 | 0.421 | 0.417 | 0.413 | 0.409 | 0.405 | 0.401 | 0.397 | 0.394 | 0.390 | 0.386 |
| 0.3 | 0.382 | 0.378 | 0.374 | 0.371 | 0.367 | 0.363 | 0.359 | 0.356 | 0.352 | 0.348 |
| 0.4 | 0.345 | 0.341 | 0.337 | 0.334 | 0.330 | 0.326 | 0.323 | 0.319 | 0.316 | 0.312 |
| 0.5 | 0.309 | 0.305 | 0.302 | 0.298 | 0.295 | 0.291 | 0.288 | 0.284 | 0.281 | 0.278 |
| 1.6 | 0.055 | 0.054 | 0.053 | 0.052 | 0.051 | 0.049 | 0.048 | 0.047 | 0.046 | 0.046 |
| 1.7 | 0.045 | 0.044 | 0.043 | 0.042 | 0.041 | 0.040 | 0.039 | 0.038 | 0.038 | 0.037 |
| 1.8 | 0.036 | 0.035 | 0.034 | 0.034 | 0.033 | 0.032 | 0.031 | 0.031 | 0.030 | 0.029 |
| 1.9 | 0.029 | 0.028 | 0.027 | 0.027 | 0.026 | 0.026 | 0.025 | 0.024 | 0.024 | 0.023 |
| 2 | 0.023 | 0.022 | 0.022 | 0.021 | 0.021 | 0.020 | 0.020 | 0.019 | 0.019 | 0.018 |
上の表の紫色セルで示した値が「0.025」です。また、この値をとるのは赤色セルと青色セルから「z=1.96」であることが分かります。したがって、標準正規分布表において上側2.5%点は「1.96」であり、負の数である「-1.96」以下の値をとる確率も2.5%となります(標準正規分布は平均値であるx=0において左右対称であるため)。したがって、標準化した値の範囲は次のように書けます。この「1.96」という値は今後もよく出てくるので覚えておくと便利です。
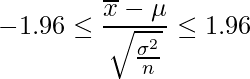
3の式を![]() について変形します。
について変形します。
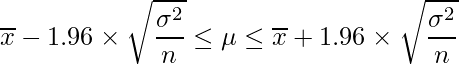
この式を用いることで、母分散がわかっている時の母平均![]() の95%信頼区間を求められます。合計スクリーン数のデータに当てはめると、
の95%信頼区間を求められます。合計スクリーン数のデータに当てはめると、
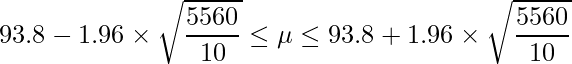
となるので、計算すると次のようになります。
【まとめ】母平均の信頼区間(母分散既知)
標本平均を![]() 、母集団の平均を
、母集団の平均を![]() 、母分散を
、母分散を![]() 、抽出したサンプルサイズをnとすると、次の式から母平均
、抽出したサンプルサイズをnとすると、次の式から母平均![]() の95%信頼区間を求めることができる。
の95%信頼区間を求めることができる。
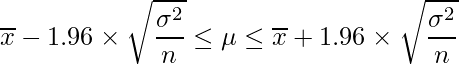
また、一般化して信頼係数![]() (=100
(=100![]() %)の場合には、標準正規分布の上側確率を用いて次のように表すことができる。
%)の場合には、標準正規分布の上側確率を用いて次のように表すことができる。![]() は標準正規分布表の上側確率が
は標準正規分布表の上側確率が![]() となる値(z値)を表す。
となる値(z値)を表す。
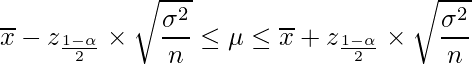
【コラム】パーセント点
ある確率分布関数において、ある値▲より大きくなる確率が☆%であるとき、この▲のことを「上側☆%点(パーセント点)」といいます。このとき、ある値▲より大きくなる確率のことを「上側確率」といいます。(ある値▲より小さくなる確率のことを「下側確率」といいます)
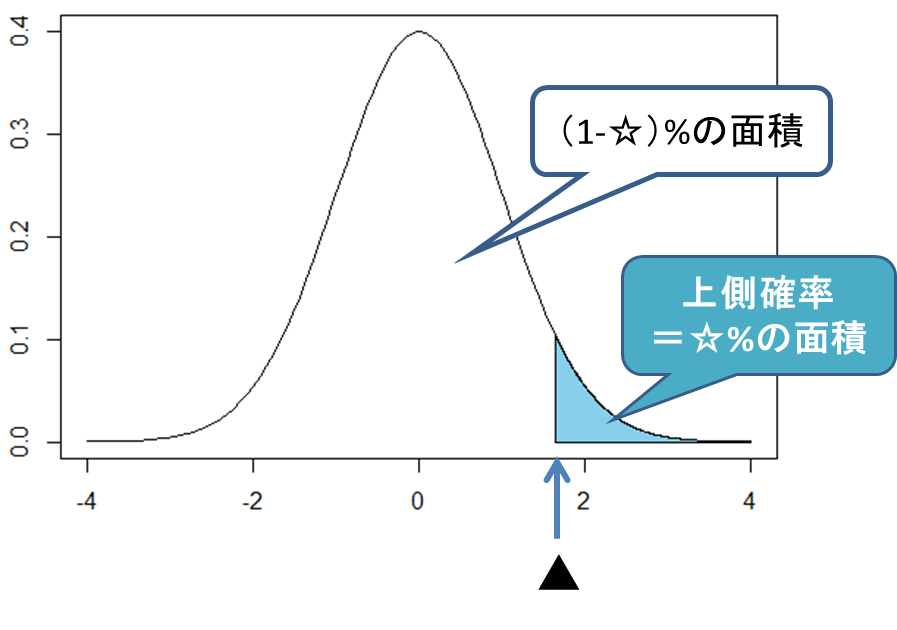
統計数値表は、さまざまな確率分布におけるある値▲とその上側確率(あるいは下側確率)をまとめた表のことです。
19. 母平均の区間推定(母分散既知)
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
母平均の区間推定(母分散未知)
- 14. いろいろな確率分布2
14-3. 標準化したデータの使い方
- 14. いろいろな確率分布2
14-4. 標準正規分布表
- 14. いろいろな確率分布2
14-5. 標準正規分布表の使い方1
- 17. 大数の法則と中心極限定理
17-3. 中心極限定理1
- 17. 大数の法則と中心極限定理
17-4. 中心極限定理2







