中心極限定理は、平均、分散に従う母集団からサンプルサイズの標本を抽出する場合、その平均値の分布はが大きくなるにつれて正規分布に近づくというものです。

中心極限定理を元にすると、サンプルサイズが大きいほど標本平均の分布における平均は母平均に、さらに標本平均の分布における標本分散は母分散（＝母集団の分散）の倍の値に近づきます。これは、サンプルサイズが大きいほどその標本平均のばらつきが小さくなり、標本平均が母平均のより近くに集まる（平均値をより正確に推測できる）ことを表しています。

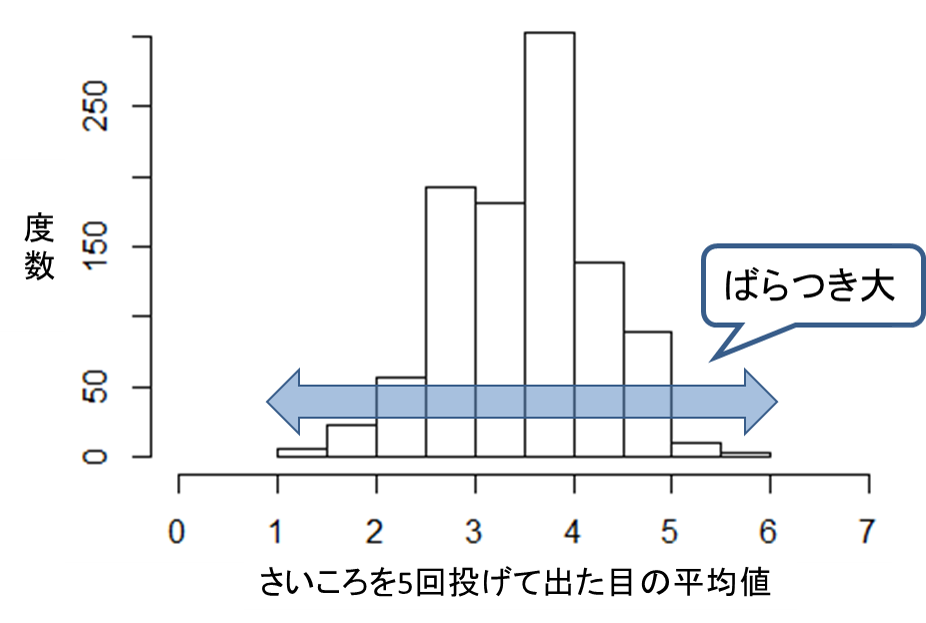
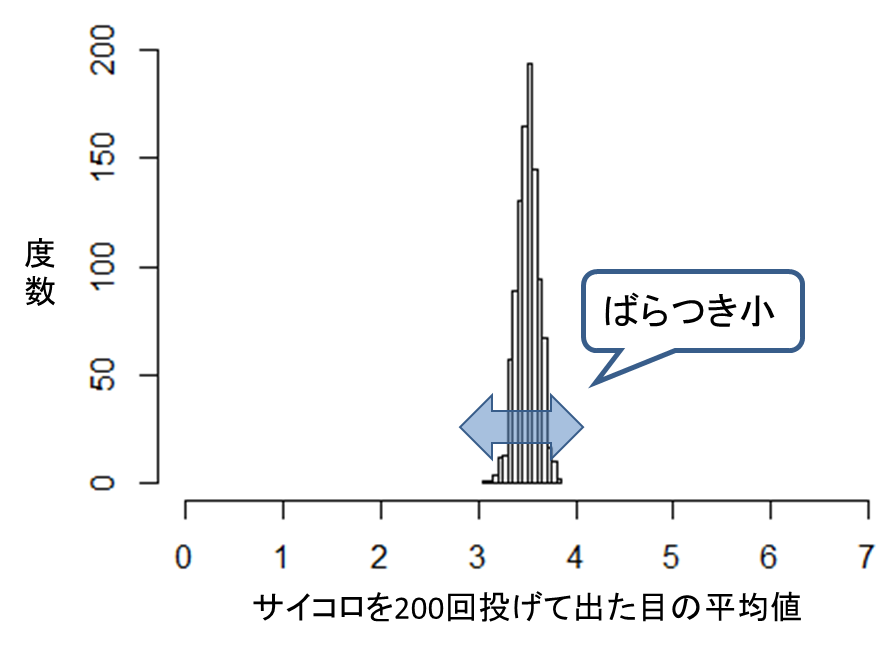
さいころを5回、および200回投げて出る目の平均値を計算するという実験を1000件行った結果が次のヒストグラムです。さいころを200回投げた場合のほうが、標本平均のばらつきが小さいことが分かります。

また、平均、分散に従う母集団からサンプルサイズの標本を抽出した場合の平均値について、標準化をおこなった値

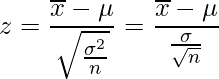
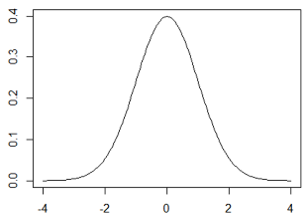
の分布はサンプルサイズが大きくなるにつれて、標準正規分布に近づきます。