※コラム「統計備忘録」の記事一覧はこちら※

統計学のテキストでは母集団の平均を母平均といってギリシャ文字の μ（ミュー）で表します。一方、母集団から抽出した標本集団の平均を標本平均といってアルファベットの小文字の m や X（エックスバー）で表します。

推測統計学（統計的仮説検定や推定のこと）の立場では母平均は1個しか存在しません。通常、母集団のすべてを調べることはできませんから、標本のデータを使って母平均を推測することになります。標本平均は余程の偶然でもない限り、サンプリングをしなおす度に値が異なります。このように都度異なる標本平均から、たった1つの母平均をどのように推測できるのでしょうか。この問題を解決してくれるのが中心極限定理 central limit theorem です。

皆さんの中には、t 検定をするとき、サンプリングしたデータが正規分布に従っているか心配で仕方がないという人がいるかもしれませんが、実のところそれほど心配する必要はありません。中心極限定理によって母集団がどんな分布であっても「標本平均の分布は正規分布に従う」ことが分かっているからです。「標本平均の分布」とは、同じ母集団から何度も無作為抽出（実験の場合は無作為化）を繰り返して、その度に計算しなおした場合の標本平均のバラツキ具合です。この標本平均の分布は、母平均 μ を中心とし母標準偏差を標本の大きさ n の二乗根で割った値（母標準偏差／√n ）を標準偏差とする正規分布になります。標本の大きさ n が大きくなるほど正規分布に近づき、n が30にもなればほぼ正規分布に一致します。なお、母標準偏差／√n のことを標準誤差というのは「標準誤差」の記事で書いたとおりです。

例えば、次のように、母平均 μ が1,927、母標準偏差 σ が 925 で平均よりも中心が左に偏った分布をしている 1万件の母集団があったとします。

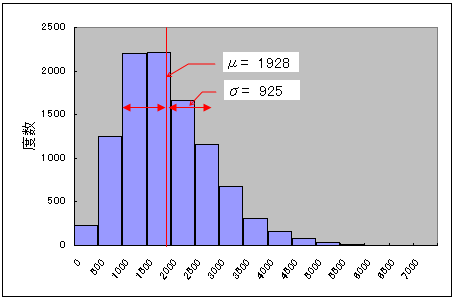
この母集団から無作為に 30 件を取り出すということを何度も繰り返し、その度に標本平均 m を求めると、m の分布は、母平均 μ を中心として標準偏差が 169（=925/√30 ）の正規分布に似たものになります。ということは、抽出を 100 回繰り返すと、そのうちの95回の標本平均は、1,927±169×1.96 の範囲におさまるだろうということです。標本平均が母平均とまったく同じということはまずないでしょうが、母平均から遠い値よりも近い値になる方が確率的には高いのです。

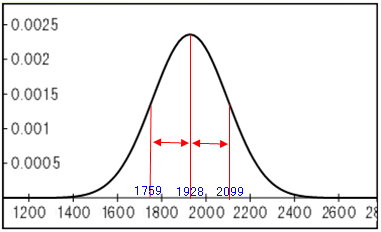
n を大きくしていくと標本平均の分布は狭まります。次のグラフは n が 30（黒線）と n が 100（赤線）の場合の標本平均の分布を示しています。n を大きくしたほうが誤差が小さくなるのも、中心極限定理で説明できます。

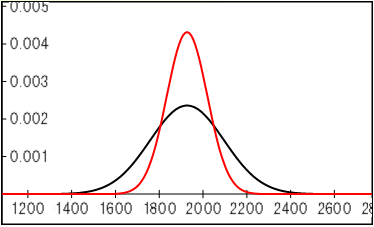
n が小さくなるにしたがって、標本平均の正規分布は崩れていきます。崩れの程度は、母集団の分布が正規分布に近いほど緩やかです。したがって、n が小さく、かつ、母集団が正規分布すると仮定できないときには、対数変換などによって正規分布に近づくように、データを変換してから t 検定や分散分析を行うかデータ変換をしないでノンパラメトリック検定を行う事も考えましょう。