交互作用とは
2017/08/19
カテゴリ:コラム「統計備忘録」
タグ:統計備忘録
※コラム「統計備忘録」の記事一覧はこちら※
私が「交絡」という言葉に初めてお目にかかったときのことですが、「交互作用」と勘違いしてしまった覚えがあります。でも、両者は別物です。英語にすれば、前者が confunding、後者が interaction ですね。今回は後者について書きます。
交互作用とは、2つ以上の要因が考えられるとき、要因が組み合わさったときにだけ現れる作用のことです。例えば、「層別分析とは」の記事中で、喫煙と飲酒と肺がんの話をしましたが、その中で、非喫煙グループでは飲酒の量と肺がんの発症には関連が無いけれど、喫煙者は非喫煙者よりも肺がんのリスクが高く、その中でも飲酒量の多い人の方がリスクが高くなるようだと書きました。これは、交互作用の中でも、交互作用がさらに作用を強めてしまう例ですね。
交互作用には作用を強めてしまうものだけでなく、作用を弱めてしまったり、反対の作用をもたらしたりというものもあります。二元配置分散分析をすると分散分析表に交互作用の検定の結果も出力されますが、分散分析表だけを見ていても、交互作用が有意になったからといって、交互作用がプラスに働いていたのかマイナスに働いていたのかは分かりません。交互作用の出方をグラフなどにして確認する必要があります。
多重ロジスティック回帰分析で交互作用の有無を確認したいのなら、説明変数の中に交互作用項を加えて分析します。飲酒と喫煙の例で説明すると、交互作用項のデータは、喫煙者でよくお酒を飲む人は1、それ以外の人は0となるようにします。Excelなら次のようにすると簡単に加工できます。
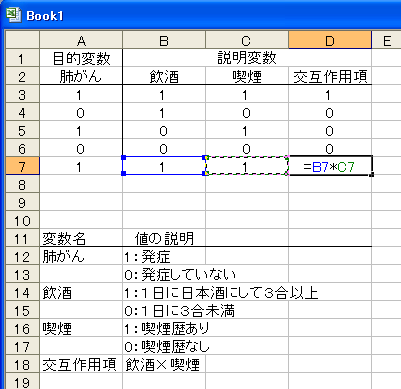
交互作用項は説明変数同士の積になっているので、「積項」とも言います。交互作用項を作ったら、喫煙の有無、飲酒量、交互作用項を説明変数(独立変数)に、肺がんの発症の有無を目的変数(従属変数、アウトカム変数)にして多重ロジスティック回帰分析にかけます。交互作用項のオッズ比が1より大きければ、肺がんのリスクを高める交互作用があるのではということになります。
さて、私が交絡を交互作用と勘違いした原因ですが、私が実験から統計学の世界に入ったことが大きいと思います。実験では、原則として、要因同士が直交するよう(独立するよう。無相関になるよう)すべての実験条件の例数を等しくします。したがって、要因間の相関係数は0が当然なので交絡とは無縁です。私が交絡の意味を理解したのは医学統計を勉強するようになってからですね。








