もう少し回数を増やして、1回から1000回までさいころを投げる、という計1,000件の実験を行い、それぞれの回数での出た目の平均値を次の図にプロットしました。このグラフを見ると、回数が増えるにつれてだんだんと出る目の平均が3.5あたりに収束していくのが分かります。

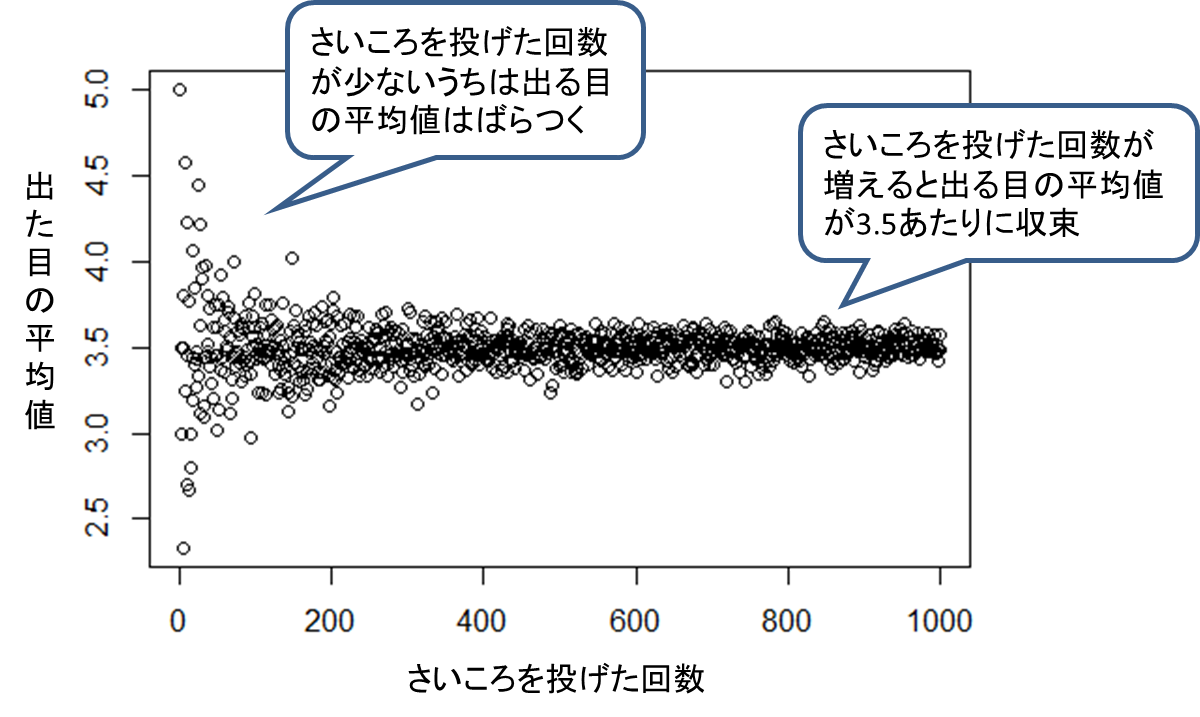
このように、さいころを投げる回数を増やすほど各目の出る回数はに近づくため、出る目の平均値は、

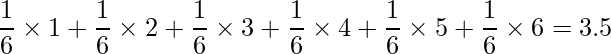
に近づくというわけです。大数の法則は「母平均がμ（ミュー）である集団から標本を抽出する場合、サンプルサイズ（＝標本の大きさ）が大きくなるにつれて、標本平均は母平均μに近づく」と言うことも出来ます。

大数の法則を元にすると、母集団から抽出された標本から母平均を推測する場合には、サンプルサイズが大きくなるほどより正確に母平均を推測できるということが分かります。