中心極限定理：

「標本を抽出する母集団が平均、分散の正規分布に従う場合においても、従わない場合においても、抽出するサンプルサイズが大きくなるにつれて標本平均の分布は「平均、分散」の正規分布 に近づく」

さいころを何回か投げて出る目の平均値を計算するという実験について考えます。さいころの1から6までの目が出る確率は全て等しいことから、一様分布に従います。

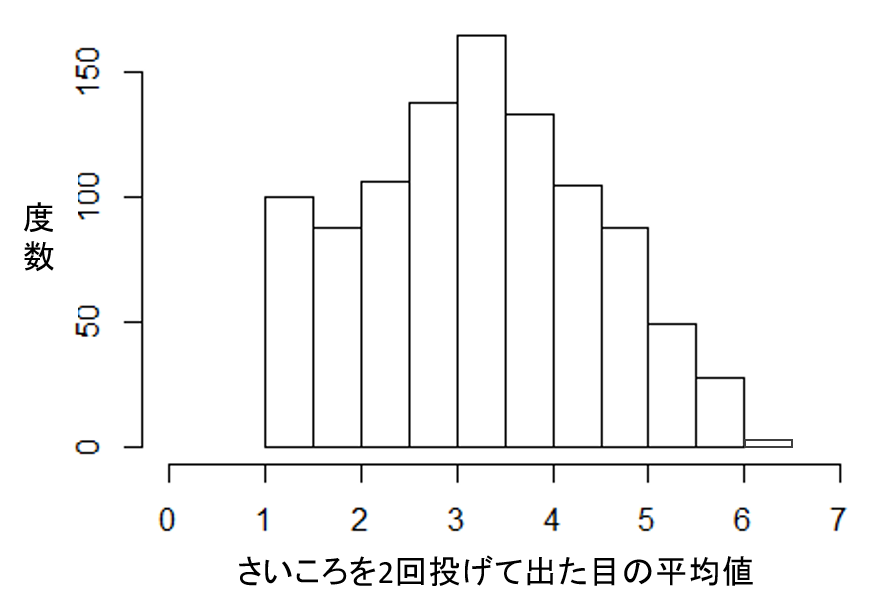
さいころを2回投げて出る目の平均値を計算するという実験を1000件行った結果をヒストグラムにすると次のようになります。このヒストグラムはさいころを2回投げて出た目の平均についての標本分布を表したものです。横軸は出た目の平均値、縦軸はその確率になります。このヒストグラムからでは、出た目の平均値は正規分布をしているとは言えなさそうです。

次に、さいころを投げる回数を5回と10回にしてみます。実験回数は先程と同じ1000件です。

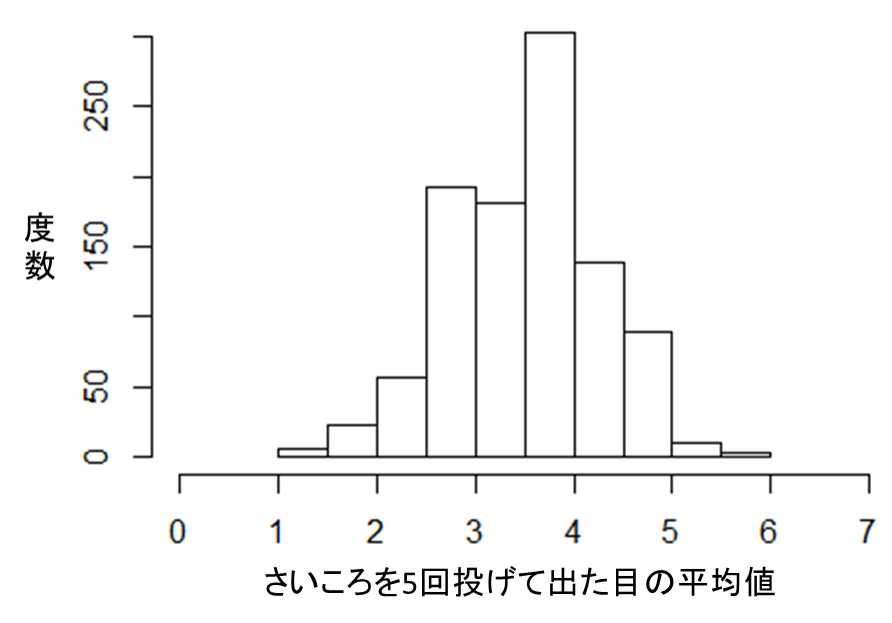
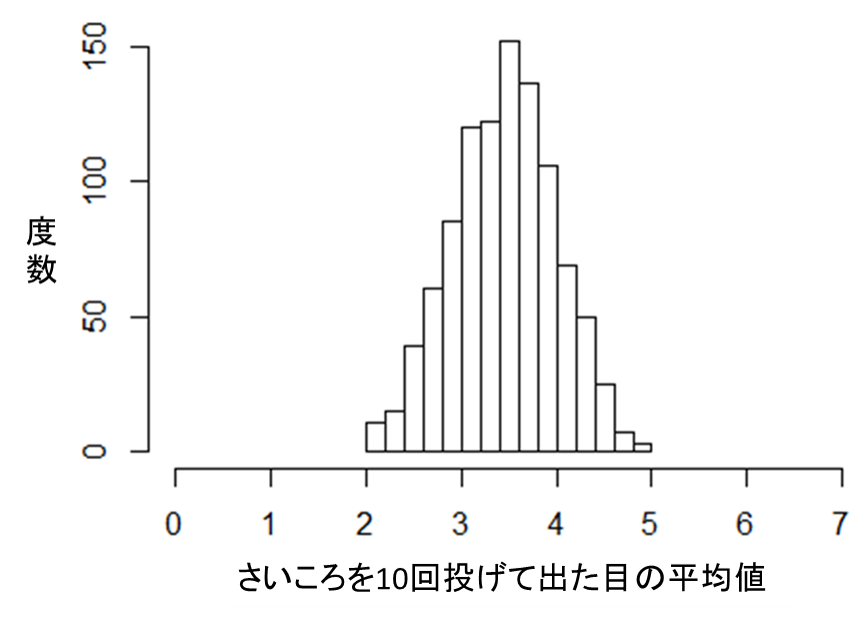
1件の実験においてさいころを投げる回数が増えるにつれ、ヒストグラムは正規分布の形に近づいてきているのが分かります。

■おすすめ書籍

上手なグラフの作り方について、子供にも分かるように書かれています。