ヒストグラムは度数分布表をグラフにしたものです。2-1章で使用した各都道府県内にある映画館のスクリーン数のデータを用いてヒストグラムを作成すると次のようになります。

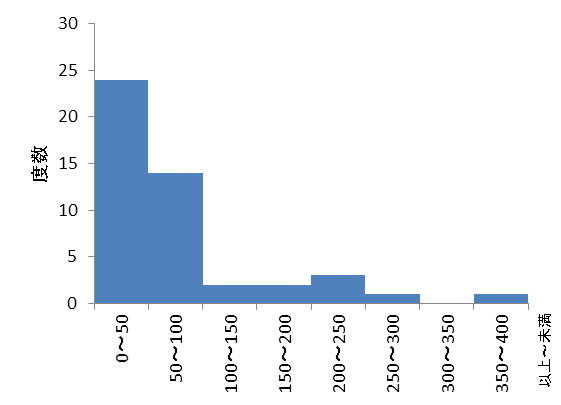
横軸は「階級」を、縦軸は「度数」を表しています。例えば、横軸が「0～50」にある棒は「スクリーン数の合計が0以上50未満の都道府県の度数」を表します。このグラフを見ると、スクリーン数の合計が0以上100未満の都道府県が大半であるということが分かります。

次に示すように、ヒストグラムの各階級の棒を度数が大きい順に左から並べ替え、その上に累積相対度数の折れ線グラフを重ねる場合もあります。このようなグラフを「パレート図」といいます。横軸は先ほどと同じ「階級」を、左側の縦軸は「度数」を、右側の縦軸は「累積相対度数」を表しています。

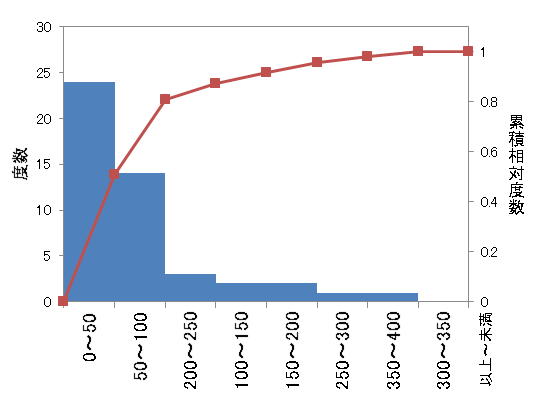
赤い折れ線グラフを見ると、スクリーン数の合計が「0以上50未満」の都道府県は全体の約50％強であることが分かります。また、スクリーン数の合計が「0以上100未満」の都道府県は全体の約80％であることが分かります。

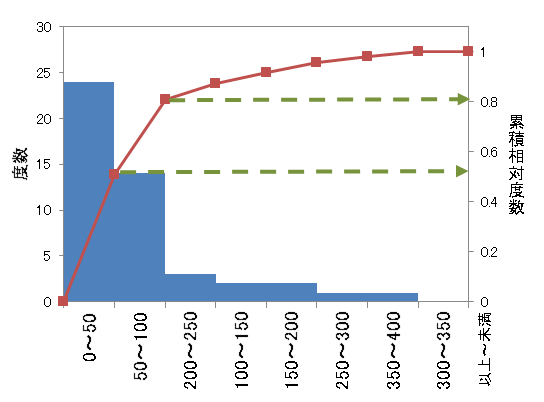
このようにヒストグラムを描くと、データの分布を視覚的に捉えることができます。例えば次の図のように、データの分布の山（度数の多い部分）が左側に偏り、右に行くにつれて山がなだらかになっている（度数が少ない）ヒストグラムのことを「右裾が長い」もしくは「右に歪んだ」もしくは「左に偏った」分布といいます。

一方、次の図のようにデータの分布の山（度数の多い部分）が右側に偏り、左に行くにつれて山がなだらかになっている（度数が少ない）ヒストグラムのことを「左裾が長い」もしくは「左に歪んだ」もしくは「右に偏った」分布といいます。

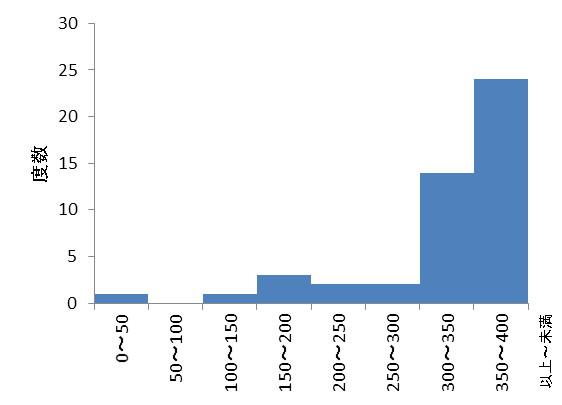
【コラム】棒グラフとヒストグラムはどのように使い分けるのか

ヒストグラムは棒グラフの"棒の隙間"を埋めただけではないのか？と思う人がいるかも知れませんが、これらは明確なちがいがあります。手元にあるデータが、1-4. 変数の尺度で学んだ「質的データ」か「量的データ」であるかによって、これらのグラフを使い分けます。

棒グラフは「質的データ」の可視化に使います。例えば、5-2. 棒グラフ・円グラフ・折れ線グラフに掲載している棒グラフのように、ある学校の定期試験の平均点のデータは棒グラフで表します。棒の高さを見て、それぞれの値を比較することができます。

一方のヒストグラムは「量的データ」の可視化に使います。量的データから作成した度数分布表をグラフにしたものがヒストグラムなので、ヒストグラムを見るとそのデータの分布を知ることができます。