- Step1. 基礎編
- 2. 度数分布とヒストグラム
2-5. ジニ係数
2つの累積相対度数を用いて描かれたローレンツ曲線を使うと、「偏り=不均等さ」を確認できます。
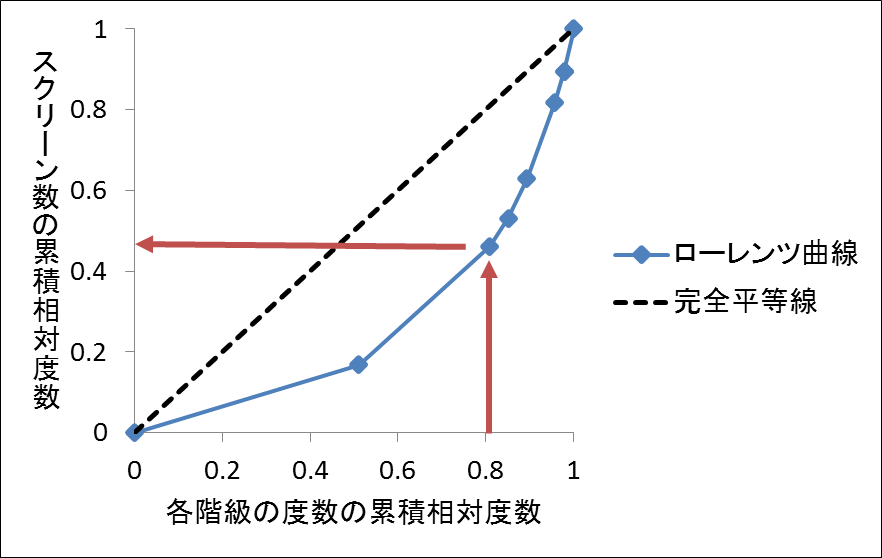
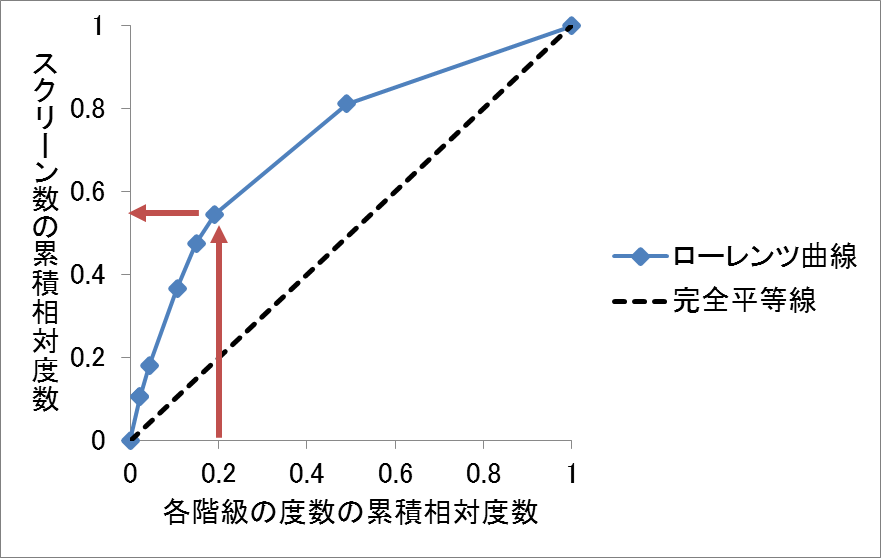
例えば、次の各都道府県内にある映画館のスクリーン数のデータから作成したローレンツ曲線の赤い矢印をたどると、約80%の都道府県内で全国のすべてのスクリーン数の40%強があるということが分かります。逆に、残りの約20%の都道府県内には60%弱ものスクリーン数があるということなので、スクリーンの分布は不均等であることが分かります。
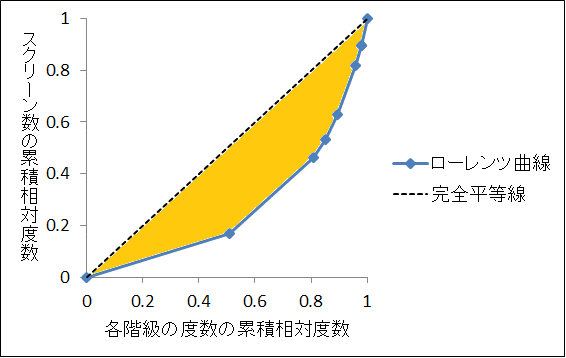
この「偏り」や「不均等さ」を数値で表したものが「ジニ係数」です。ジニ係数は完全平等線((0,0)と(1,1)を結ぶ線:図中の黒破線)とローレンツ曲線との間の面積(次の図の橙色部分)を2倍した値になります。ジニ係数は0から1までの値をとり、1に近いほど偏りが大きく、0に近いほど偏りが小さいことを表します。
■ジニ係数が0の場合
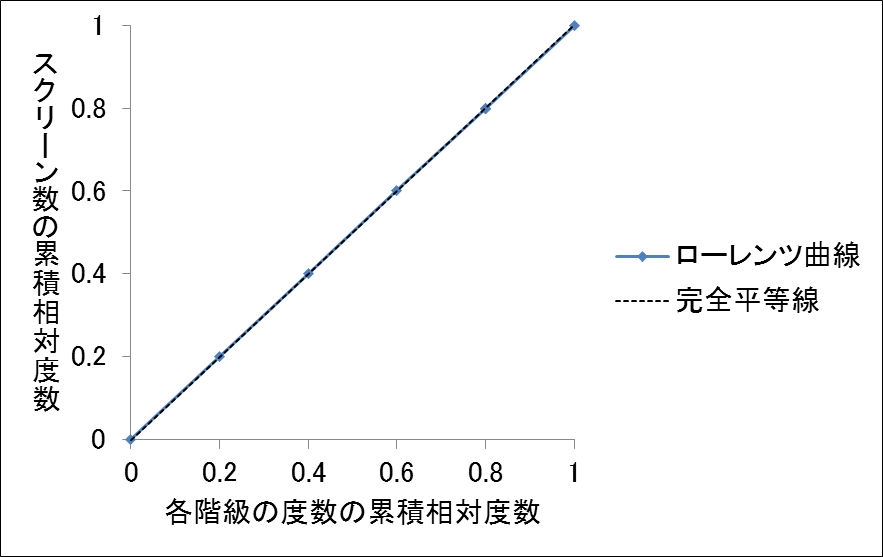
不均等さが全くない場合、ローレンツ曲線は次の図のように完全平等線と一致するためジニ係数は「0」となります。ジニ係数が0というのは、ここでは各都道府県内にあるスクリーン数が全て同じ場合、すなわち「20%の都道府県内に全国の総スクリーン数の20%があり、40%の都道府県内に全国の総スクリーン数の40%があり…」という状態を指します。
■ジニ係数が1に限りなく近づく場合
一方、例えば東京都(1/47=2.1%)に日本の全ての映画館(スクリーン)があり、他の道府県(46/47=97.9%)に映画館(スクリーン)が全くない場合、ローレンツ曲線は次のようになります。このときジニ係数は「0.979」となります。
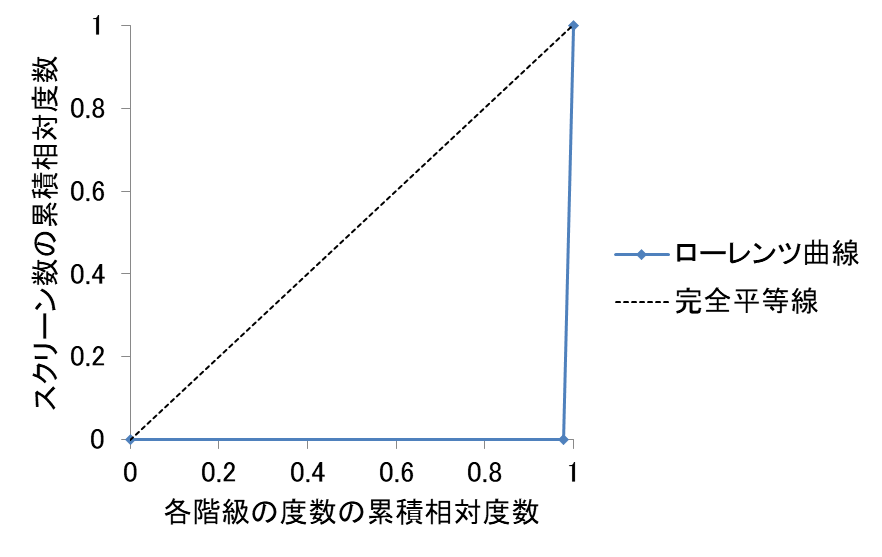
■ジニ係数が1になる場合
例えば日本に映画館を管理する会社が1社しかなく、その会社(100%)が日本のすべての映画館(100%)を管理している場合、ローレンツ曲線は次のようになります。このときジニ係数は最大値の「1」となります。
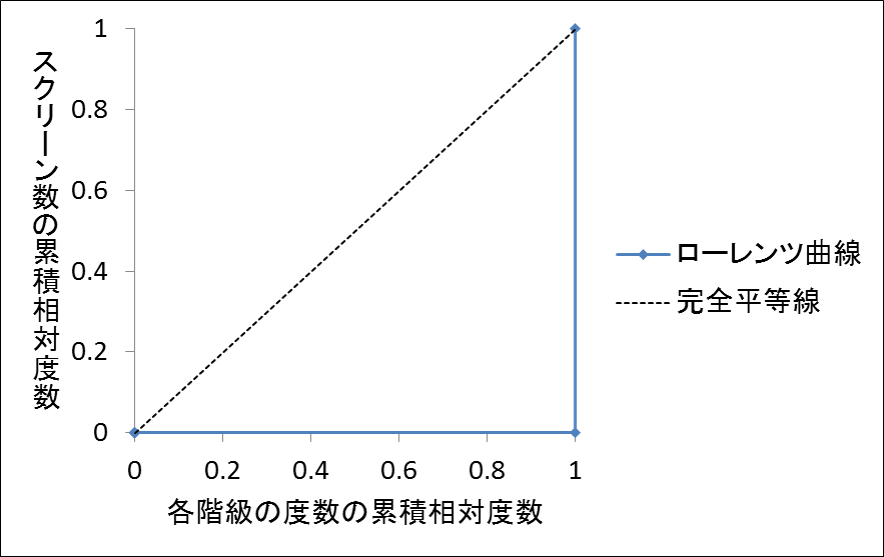
【コラム】ローレンツ曲線は下側凸か上側凸か
ローレンツ曲線を描くとき、一般的に階級を小さい順(昇順)に並べた場合の2つの累積相対度数を用います。そのため、よく目にするローレンツ曲線は完全平等線に対して下側に凸となっています。
一方、スクリーン数の集中度を見たい場合には、下の表のように階級を大きい順に並べたものを用いることがあります。
| 階級 | 度数 | 各階級の度数の 累積相対度数 | 各階級の スクリーン数合計 | スクリーン数の 相対度数 | スクリーン数の 累積相対度数 |
|---|---|---|---|---|---|
| 350以上400未満 | 1 | 0.0213 | 358 | 0.1042 | 0.1042 |
| 300以上350未満 | 0 | 0.0213 | 0 | 0.0000 | 0.1042 |
| 250以上300未満 | 1 | 0.0426 | 258 | 0.0751 | 0.1793 |
| 200以上250未満 | 3 | 0.1064 | 641 | 0.1865 | 0.3658 |
| 150以上200未満 | 2 | 0.1490 | 377 | 0.1097 | 0.4755 |
| 100以上150未満 | 2 | 0.1916 | 239 | 0.0695 | 0.5450 |
| 50以上100未満 | 14 | 0.4895 | 918 | 0.2670 | 0.8120 |
| 0以上50未満 | 24 | 1.0000 | 646 | 0.1880 | 1.0000 |
| 合計 | 47 | - | 3437 | 1.0000 | - |
この場合のローレンツ曲線は、次に示すように完全平等線に対して上側に凸となります。このローレンツ曲線を見ると、約20%の都道府県内に60%弱ものスクリーン数があることが読み取れます。
■おすすめ書籍
コア・テキスト統計学は経済学をベースに書かれている統計入門書なので、ローレンツ曲線やジニ係数、経済指標についての説明が比較的充実しています。
2. 度数分布とヒストグラム
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 2. 度数分布とヒストグラム
2-1. 度数分布と累積度数分布
- 2. 度数分布とヒストグラム
2-4. ローレンツ曲線