- Step1. 基礎編
- 2. 度数分布とヒストグラム
2-6. ジニ係数の求め方
次の図のローレンツ曲線から「ジニ係数」を求めてみます。ジニ係数は完全平等線((0,0)と(1,1)を結ぶ線:図中の黒破線)とローレンツ曲線との間の面積(橙色部分)を2倍した値です。
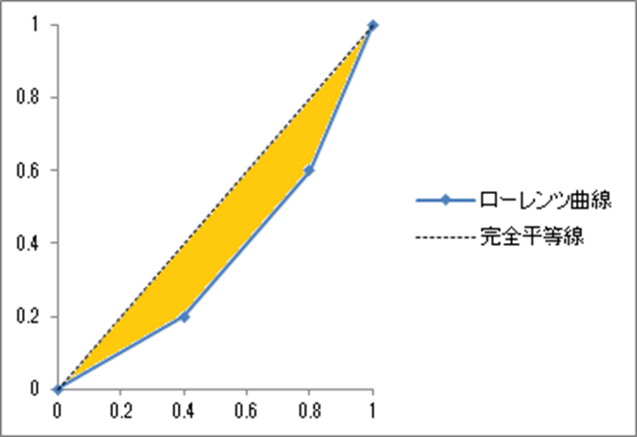
このローレンツ曲線は次の表のデータから作成しています。
| 累積相対度数(横軸) | 累積相対度数(縦軸) |
|---|---|
| 0 | 0 |
| 0.4 | 0.2 |
| 0.8 | 0.6 |
| 1 | 1 |
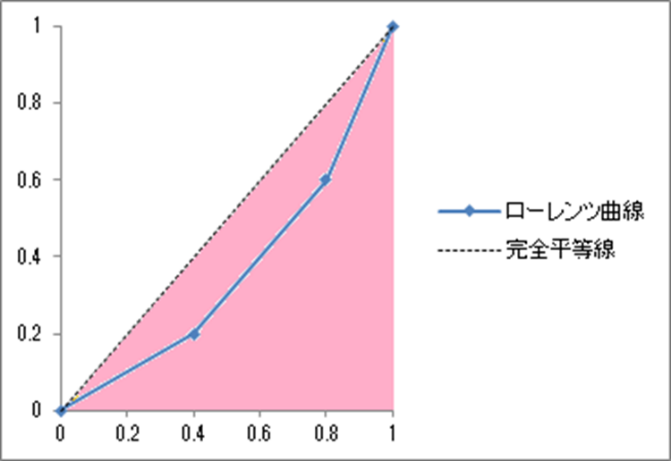
まず、完全平等線とx軸(横軸)とで囲まれた部分の面積(次の図のピンク色部分)を求めます。底辺が「1」、高さが「1」の三角形なので、![]() となります。
となります。
次に、ローレンツ曲線とx軸(横軸)とで囲まれた部分の面積を求めます。この面積は、3つに分割して考えます。
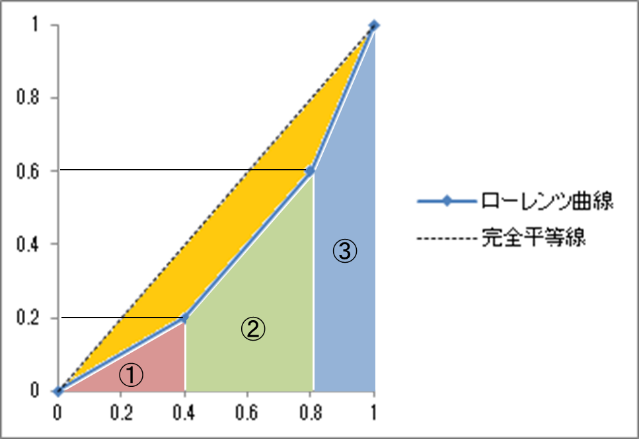
①:底辺が「0.4」、高さが「0.2」の三角形なので、![]() となります。
となります。
②:90度回転させて考えます。上底が「0.2」、下底が「0.6」、高さが「![]() 」の台形なので、
」の台形なので、![]() となります。
となります。

③:同様に、下のように90度回転させて考えます。上底が「0.6」、下底が「1」、高さが「1-0.8=0.2」の台形なので、![]() となります。
となります。

①②③を全て足すと![]() となります。
ピンク色の面積0.5からこれら①②③の面積を引いた
となります。
ピンク色の面積0.5からこれら①②③の面積を引いた![]() が、橙色の部分の面積になります。したがって、0.14を2倍にした
が、橙色の部分の面積になります。したがって、0.14を2倍にした![]() がジニ係数となります。
がジニ係数となります。
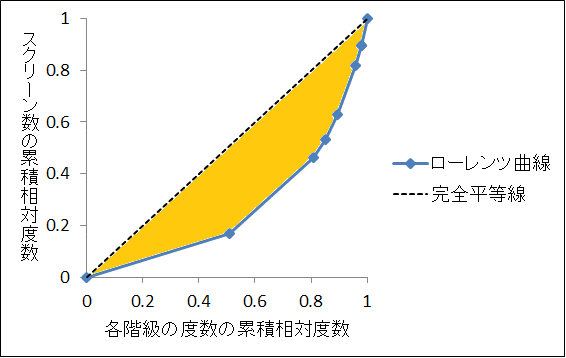
同様にして次の図の都道府県ごとのスクリーン数のデータを元に2‐4章で作成したローレンツ曲線からジニ係数を求めると「0.466」になります。
■おすすめ書籍
コア・テキスト統計学は経済学をベースに書かれている統計入門書なので、ローレンツ曲線やジニ係数、経済指標についての説明が比較的充実しています。
2. 度数分布とヒストグラム
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 2. 度数分布とヒストグラム
2-4. ローレンツ曲線
- 2. 度数分布とヒストグラム
2-5. ジニ係数







