- 17. 大数の法則と中心極限定理
練習問題(17. 大数の法則と中心極限定理)
1
コインを投げ、表が出た割合を計算する。気の遠くなるほど投げ続けた時、表が出た割合はおよそどれくらいになると考えられるか。

答えを見る
- 答え
 閉じる
閉じる -
大数の法則より、観測したデータから計算した表が出た割合
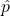 は、コインで表が出る確率
は、コインで表が出る確率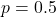 に収束します。よって、表が出た割合は0.5に近づくと考えられます。
に収束します。よって、表が出た割合は0.5に近づくと考えられます。
2
平均![]() 、分散
、分散![]() のある分布に従う、互いに独立なn個の確率変数
のある分布に従う、互いに独立なn個の確率変数![]() がある。
がある。
![]() 、
、![]() を次のように定義するとき、それぞれの分散
を次のように定義するとき、それぞれの分散![]() 、
、![]() を求めよ。
を求めよ。
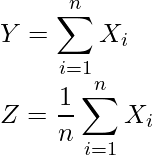

答えを見る
- 答え
 閉じる
閉じる -
確率変数の定数倍した場合の分散について次の性質(1)が成り立ちます。また、互いに独立な確率変数の分散について、次の性質(2)が成り立ちます。この2つは分布に関係なく成り立ちます(詳しくは12-6. 分散の性質をご覧ください)。
(1)
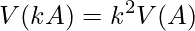
(2)
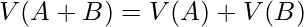
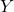 については、性質(2)を用いて次のように計算できます。
次に
については、性質(2)を用いて次のように計算できます。
次に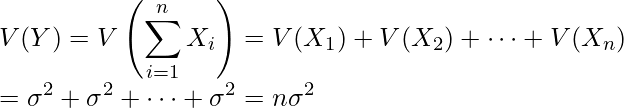
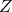 については、
については、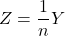 であることから、性質(1)を用いて次のように計算できます。
であることから、性質(1)を用いて次のように計算できます。
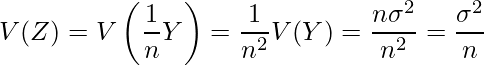
3
どのような分布に従うか不明であるが、平均![]() 、分散は
、分散は![]() の分布に従う確率変数
の分布に従う確率変数![]() がある。この確率変数n個の和を標準化したものを
がある。この確率変数n個の和を標準化したものを![]() とおく。nが非常に大きい場合、
とおく。nが非常に大きい場合、![]() はどのような分布に従うか。なお、
はどのような分布に従うか。なお、![]() は次のように計算されるものとする。
は次のように計算されるものとする。
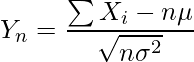

答えを見る
- 答え
 閉じる
閉じる -
中心極限定理により、
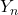 は標準正規分布
は標準正規分布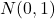 に従うと言えます。中心極限定理によると、確率変数
に従うと言えます。中心極限定理によると、確率変数 が具体的にどのような分布に従うか不明であっても、平均や分散が分かる場合には和の分布は正規分布に従うと考えられるためです。
が具体的にどのような分布に従うか不明であっても、平均や分散が分かる場合には和の分布は正規分布に従うと考えられるためです。







