日本に住む女性の平均身長を調べる場合、女性全員の身長をすべて測定するのは現実的ではないため、無作為に抽出した一部の女性の身長を測定し、その値を元に日本に住む女性全員の平均身長を推測することになります。では、母集団から無作為に選ばれた標本の平均身長は母集団の平均とぴったり同じになるでしょうか？

例えば次の図では、13人の女性からなる母集団のうち3人の女性を標本として無作為抽出し、その標本の平均を算出しています。青枠で囲まれた3人が選ばれた場合の平均は160cmとなりますが、赤枠・緑枠で囲まれた3人が選ばれた場合はそれぞれ164.3cm、131.3cmとなります。つまり、標本に誰を選ぶかによって標本の平均は様々な値となります。

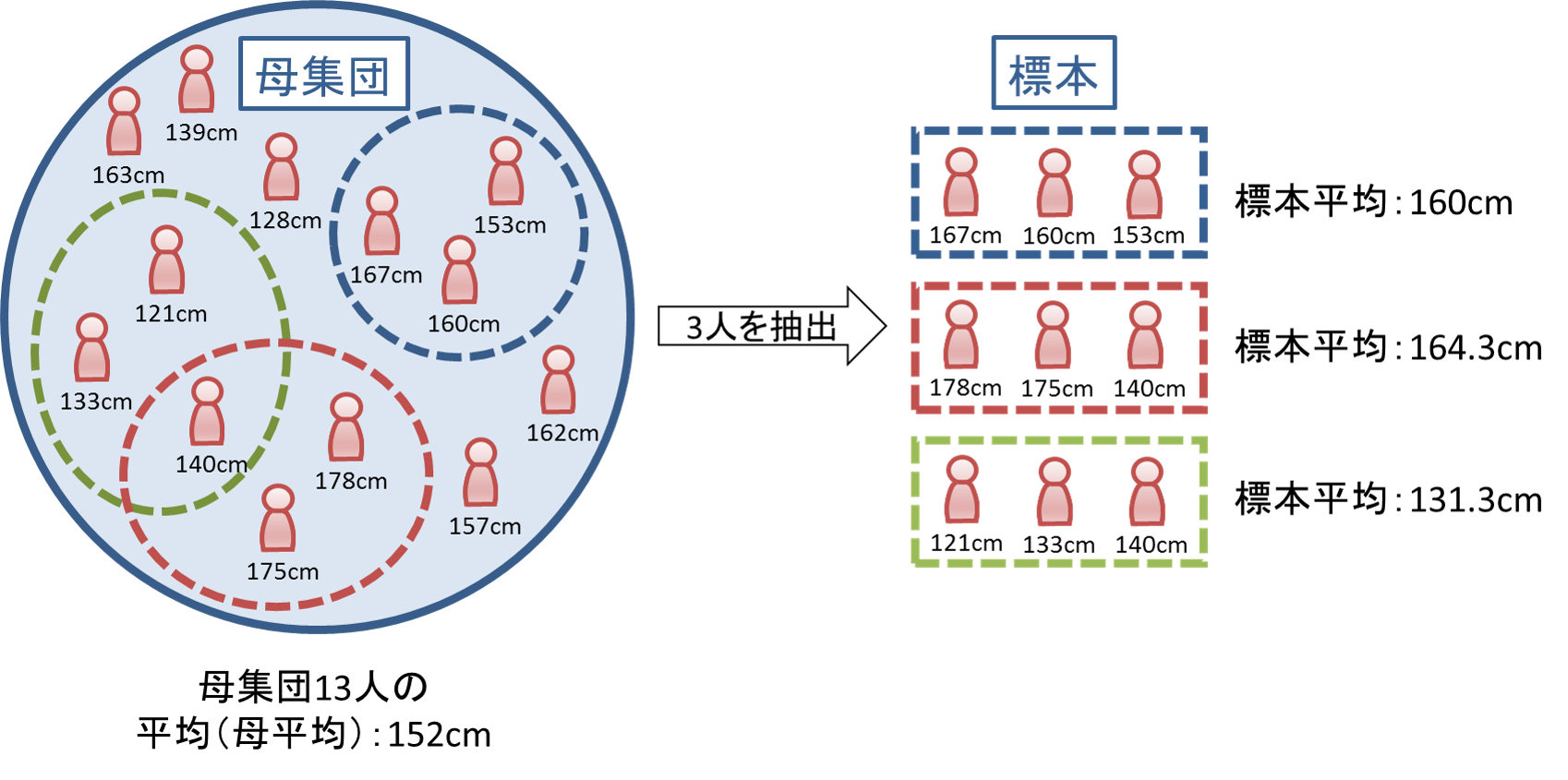
したがって、母集団から無作為に標本を選んできてその平均値を求めるということを繰り返したとしても、標本の平均（＝標本平均）は毎回ぴったりと母集団の平均（＝母平均）に一致することはなく、母平均のあたりを中心としたある程度のばらつきをもって分布すると予想されます。この分布を平均についての「標本分布」といいます。「標本分布」には幾つかの特性があり、この特性を利用して母平均を推測できます。

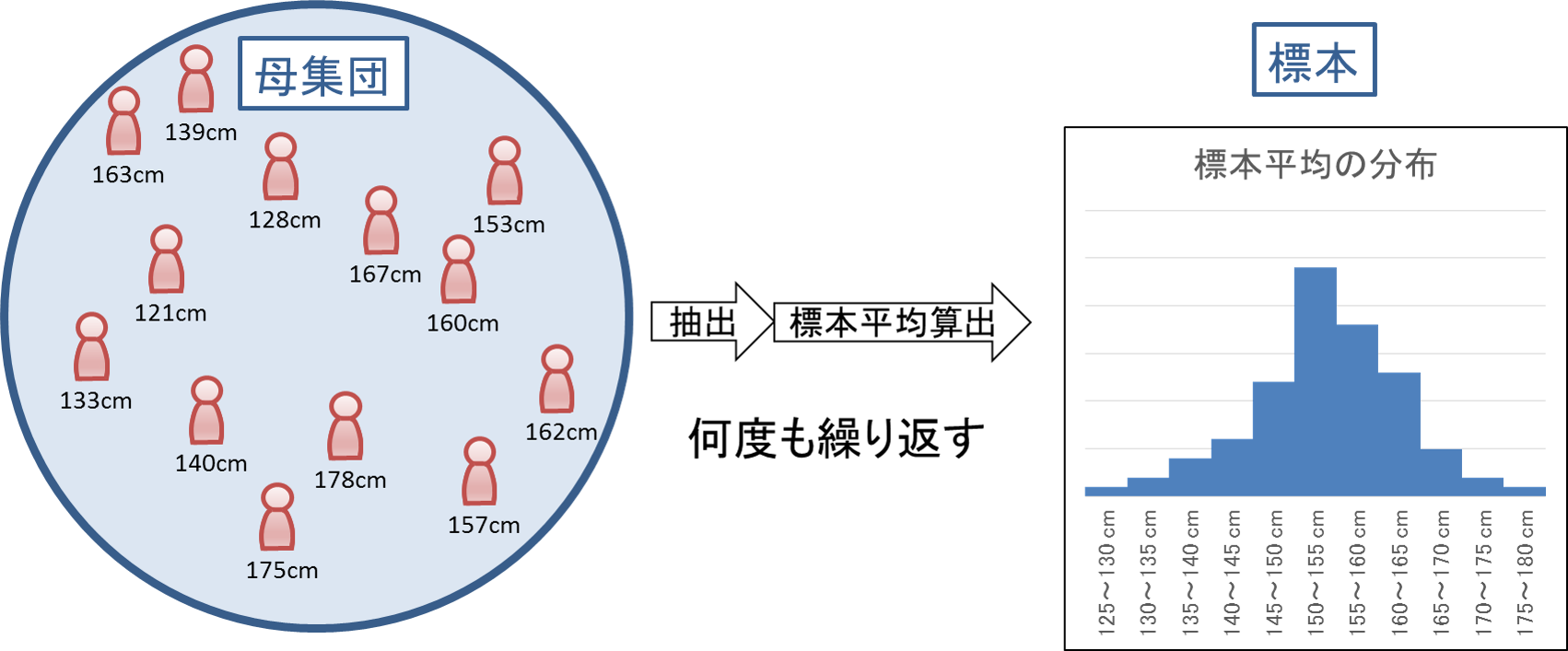
母平均を推測するためのヒントとなる法則が「大数の法則（たいすうのほうそく）」と「中心極限定理」です。この章ではまず「大数の法則」について説明します。

大数の法則：

確率pで起こる事象において、試行回数を増やすほど、その事象が実際に起こる確率はpに近づく

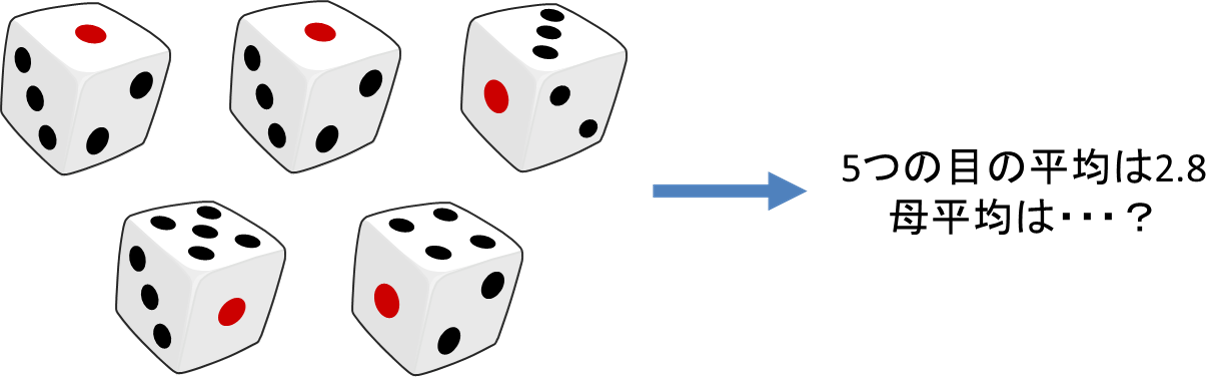
さいころを無限回数投げるとき、出る目は無限母集団となります。この無限母集団の母平均について考えてみます。さいころの出る目の平均値はだから、母平均は3.5だろうと予測できるかもしれませんが、果たして正しいと言えるでしょうか。

1回さいころを投げる、2回さいころを投げる、…、10回さいころを投げる、という計10件の実験を行い、それぞれの回数さいころを投げた時の出た目の平均値を下の図にプロットしました。横軸はさいころを投げた回数、縦軸はその回数の時の出た目の平均値です。例えば、10回投げて出た目の和は41だったので、平均値は4.1になっています。

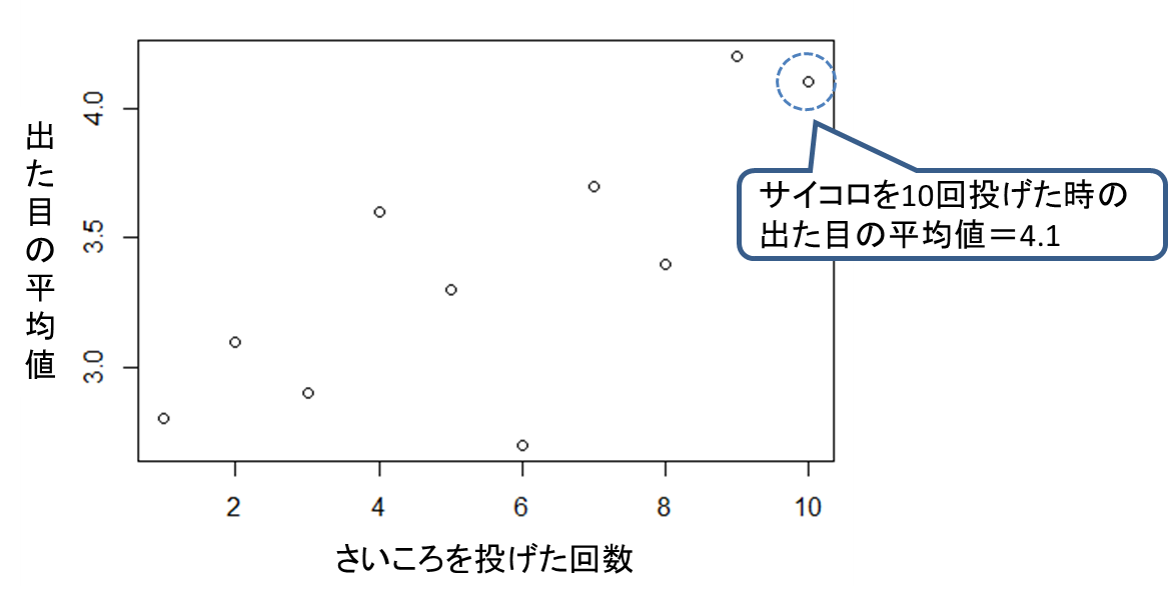
このグラフを見ると、さいころの出る目の平均は3から4の間にあるような気がしますが、3.5とは断言できないような散らばり方になっています。

■おすすめ書籍

大数の法則をもとにした読み物です。