- 19. 母平均の区間推定(母分散既知)
練習問題(19. 母平均の区間推定(母分散既知))
1
日本人男性100人をランダムに選んで身長を測定したところ、平均値は172cmであった。日本人男性の平均身長の95%信頼区間を求めよ。
ただし、日本人男性の身長の母分散は![]() であるとし、日本人男性の身長は正規分布に従うものとする。
であるとし、日本人男性の身長は正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
標準正規分布における上側2.5%点は1.96であることから、信頼区間は次のようになります。
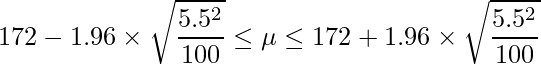
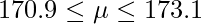
2
日本人男性100人をランダムに選んで体重を測定したところ、平均値は67kgであった。日本人男性の平均体重の90%信頼区間を求めよ。
ただし、日本人男性の体重の母分散は![]() であるとし、日本人男性の体重は正規分布に従うものとする。
であるとし、日本人男性の体重は正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
標準正規分布における上側5%点は1.64であることから、信頼区間は次のようになります。
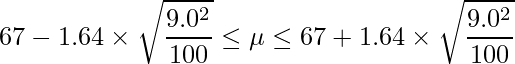
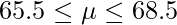
3
日本人女性400人をランダムに選んで身長を測定したところ、平均値は158cmであった。平均身長の95%信頼区間を求めよ。
ただし、日本人女性の身長の母分散は![]() であるとし、日本人女性の身長は正規分布に従うものとする。
であるとし、日本人女性の身長は正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
標準正規分布における上側2.5%点は1.96であることから、信頼区間は次のようになります。
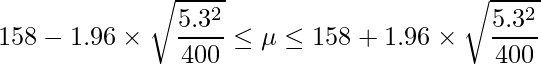
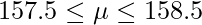
4
日本人女性100人をランダムに選んで体重を測定したところ、平均値は49kgであった。日本人女性の平均体重の99%信頼区間を求めよ。
ただし、日本人女性の体重の母分散は![]() であるとし、日本人女性の体重は正規分布に従うものとする。
であるとし、日本人女性の体重は正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
標準正規分布における上側0.5%点は2.58であることから、信頼区間は次のようになります。
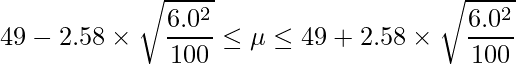
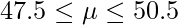
5
区間推定について述べられた文章のうち、正しいものを選べ。
- 信頼係数は自由に設定してよい
- 標本から推定された母平均の95%信頼区間の中には、95%の確率で母平均が含まれている
- 信頼係数が小さいほど、信頼区間の幅は広くなる
- サンプルサイズと信頼区間には全く関係がない

答えを見る
- 答え
 閉じる
閉じる -
- ◯:正しいです。信頼係数は自由に設定することができます。一般的には90%、95%、99%が使われます。
- ×:母平均の95%信頼区間は「母集団から標本を取ってきて、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」と解釈できます。
- ×:信頼係数が小さいほど、信頼区間の幅は狭くなります。
- ×:サンプルサイズが大きいほど、信頼区間の幅は狭くなります。







