- Step1. 基礎編
- 19. 母平均の区間推定(母分散既知)
19-4. さまざまな信頼区間(母分散既知)
各都道府県にある映画館の合計スクリーン数のデータから、次の表のようにランダムに10都道府県のデータを抽出しました。このデータを用いて、信頼係数をさまざまに変化させた場合の信頼区間を比較してみます。ただし、このデータでは母分散が![]() =5560であることが分かっており、スクリーン数の分布は正規分布に従うものとします。
=5560であることが分かっており、スクリーン数の分布は正規分布に従うものとします。
| No. | 都道府県 | 全スクリーン数 |
|---|---|---|
| 1 | 兵庫 | 126 |
| 2 | 大阪 | 224 |
| 3 | 奈良 | 34 |
| 4 | 岩手 | 25 |
| 5 | 千葉 | 199 |
| 6 | 茨城 | 89 |
| 7 | 福岡 | 178 |
| 8 | 山梨 | 14 |
| 9 | 滋賀 | 38 |
| 10 | 鳥取 | 11 |
| ― | 平均 | 93.8 |
■信頼係数による信頼区間
- 信頼係数90%のとき
- 信頼係数95%のとき
- 信頼係数99%のとき
標準正規分布において上側5%点は「1.64」であることから、次のようになります。
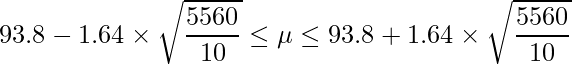
標準正規分布において上側2.5%点は「1.96」であることから、次のようになります。
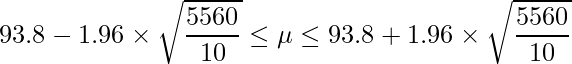
標準正規分布において上側0.5%点は「2.58」であることから、次のようになります。
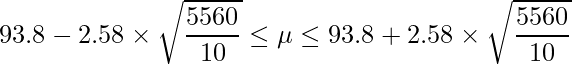
ここまでの結果をまとめると次の表のようになります。この結果から、信頼係数が大きいほど、信頼区間の幅は広くなることが分かります。
| 信頼係数 | 信頼区間 |
|---|---|
| 90% | 55.1 |
| 95% | 47.6 |
| 99% | 33.0 |
■サンプルサイズによる信頼区間
標本平均が同じであると仮定したときに、サンプルサイズを変化させた場合の信頼区間を比較してみます。信頼係数は95%とします。
- サンプルサイズが10のとき
- サンプルサイズが100のとき
- サンプルサイズが1000のとき
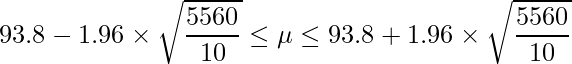
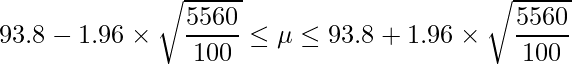
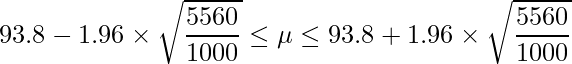
ここまでの結果をまとめると次の表のようになります。この結果から、サンプルサイズnが大きいほど、信頼区間の幅は狭くなることが分かります。
| サンプルサイズ | 信頼区間 |
|---|---|
| 10 | 47.6 |
| 100 | 79.2 |
| 1000 | 89.2 |







