- Step1. 基礎編
- 18. 母平均の点推定
18-5. 標準偏差と標準誤差
母平均の点推定を行うと、「不偏分散」のほかに「標準偏差」と「標準誤差」が出力されます。
■標準偏差
標準偏差は母集団から得られた個々のデータのばらつきを表すものであり、分散の正の平方根で定義されます。不偏分散が次の式から求められることは、18‐4章で既に学びました。
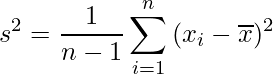
得られたデータの平均を![]() 、個々のデータを
、個々のデータを![]() 、サンプルサイズをnとすると、母集団から抽出された標本を元に推定される標準偏差
、サンプルサイズをnとすると、母集団から抽出された標本を元に推定される標準偏差![]() は次の式から求められます。
は次の式から求められます。
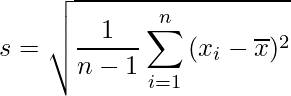
■標準誤差
標準誤差(SE:standard error)は推定量の標準偏差であり、標本から得られる推定量そのもののバラつき(=精度)を表すものです。標準誤差は、一般的に「標本平均の標準偏差」を意味します。
17‐4章ですでに学びましたが、平均μ、分散![]() に従う母集団からサンプルサイズnの標本を抽出する時、その平均値
に従う母集団からサンプルサイズnの標本を抽出する時、その平均値![]() の分布はnが大きくなるにつれて正規分布
の分布はnが大きくなるにつれて正規分布![]() に近づきます(これを中心極限定理といいます)。すなわち、サンプルサイズが大きくなるにつれて標本平均の標準偏差は
に近づきます(これを中心極限定理といいます)。すなわち、サンプルサイズが大きくなるにつれて標本平均の標準偏差は
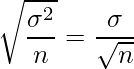
に近づきます。ただし、標本の分散は母分散![]() ではなく不偏分散
ではなく不偏分散![]() を用いることから、標本平均の標準偏差(=標準誤差SE)は標準偏差sを用いて次の式から計算できます。
を用いることから、標本平均の標準偏差(=標準誤差SE)は標準偏差sを用いて次の式から計算できます。
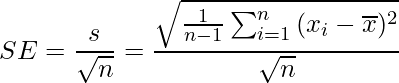
標準誤差は、母集団から抽出された標本から標本平均を求める場合、標本平均の値が母平均に対してどの程度ばらついているかを表すものです。サンプルサイズが大きくなると標準誤差は小さくなります。
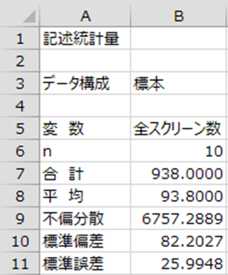
無作為に抽出された10都道府県の合計スクリーン数のデータから標準誤差を求めてみます。
| No. | 都道府県 | 全スクリーン数 |
|---|---|---|
| 1 | 兵庫 | 126 |
| 2 | 大阪 | 224 |
| 3 | 奈良 | 34 |
| 4 | 岩手 | 25 |
| 5 | 千葉 | 199 |
| 6 | 茨城 | 89 |
| 7 | 福岡 | 178 |
| 8 | 山梨 | 14 |
| 9 | 滋賀 | 38 |
| 10 | 鳥取 | 11 |
まず、標準偏差を計算すると次のようになります。
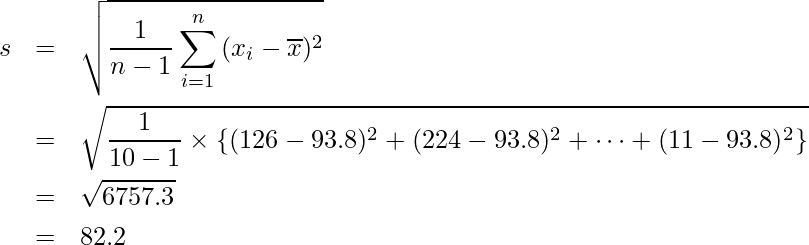
したがって標準誤差は
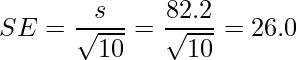
となります。
■おすすめ書籍
統計学基礎をまずはじめに勉強するための王道本だと思います。コレ1冊で統計検定®2級の範囲すべてを網羅しているわけではありませんが、統計学とはどういうものかをしっかり勉強するのに最適です。
18. 母平均の点推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 17. 大数の法則と中心極限定理
17-3. 中心極限定理1
- 17. 大数の法則と中心極限定理
17-4. 中心極限定理2
- ブログ
標準誤差
- ブログ
不偏分散の平方根は標準偏差の不偏推定量か








