- Step1. 基礎編
- 20. 母平均の区間推定(母分散未知)
20-6. 母平均の差の信頼区間
19-2章と20-3章で既に学んだ母平均の信頼区間と同様に、2つの異なる母集団の平均の差(=母平均の差)の信頼区間も算出できます。ただし、2つのデータが「対応のあるデータ」か「対応のないデータ」かによって算出方法が異なります。
対応があるデータは同じ対象に対する2つのデータのことで、データがペアになっているものを指します。そのため、2つのデータのサンプルサイズは必ず等しくなります。一方、対応がないデータは2つのデータの対象についてペアではない(無関係である)ものを指します。2つのデータのサンプルサイズは等しくない場合もあります。
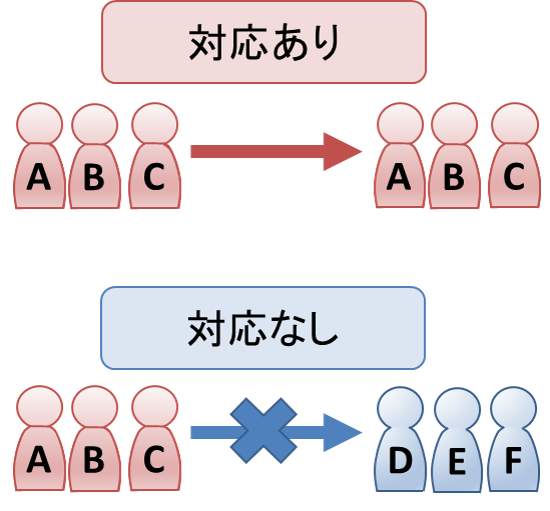
■対応があるデータの場合
あるクラスからランダムに選んだ5人の生徒の1学期と2学期の数学のテスト結果を次の表にまとめました。このデータから母平均の差の95%信頼区間を求めてみます。ただし、各学期の数学のテストの点数はそれぞれ異なる正規分布に従うものとします。
| 名前 | 1学期のテスト(点) | 2学期のテスト(点) | 1学期と2学期の差(点) |
|---|---|---|---|
| Aさん | 90 | 95 | -5 |
| Bさん | 85 | 90 | -5 |
| Cさん | 50 | 70 | -20 |
| Dさん | 75 | 60 | 15 |
| Eさん | 85 | 65 | 20 |
| 平均 | 77 | 76 | 1 |
| 不偏分散 | 257.5 | 242.5 | 267.5 |
- それぞれのデータ差の平均値と不偏分散を求めます。この例題の場合、差の平均値
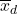 =1、不偏分散
=1、不偏分散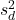 =267.5となります。
=267.5となります。 - 抽出したサンプルサイズをn、信頼係数を
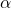 (=100
(=100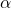 %)とすると、次の式から母平均の差
%)とすると、次の式から母平均の差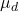 の95%信頼区間を求められます。ただし、「
の95%信頼区間を求められます。ただし、「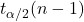 」は「自由度が
」は「自由度が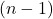 、信頼係数が
、信頼係数が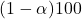 %のときのt分布表の値を示します。
%のときのt分布表の値を示します。
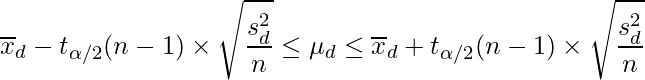
このデータの場合、サンプルサイズはn=5となります。t分布において自由度が5-1=4のときの上側2.5%点は「2.776」です。数学のテスト結果のデータを上の式に当てはめると、
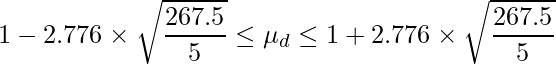
となるので、計算すると次のようになります。
■対応がないデータの場合
1組の生徒30人からランダムに選んだ5人と2組の生徒35人からランダムに選んだ4人の数学のテスト結果を次の表にまとめました。このデータから母平均の差の95%信頼区間を求めてみます。ただし、各クラスの数学のテストの点数はそれぞれ異なる正規分布に従うものとします。
| 1組の名前 | 1組の数学のテスト(点) | 2組の名前 | 2組の数学のテスト(点) |
|---|---|---|---|
| Aさん | 90 | Fさん | 95 |
| Bさん | 85 | Gさん | 90 |
| Cさん | 50 | Hさん | 70 |
| Dさん | 75 | Iさん | 60 |
| Eさん | 80 | ― | ― |
| 平均 | 76 | 平均 | 78.75 |
| 不偏分散 | 242.5 | 不偏分散 | 272.9 |
この例題で使用する記号を次のように定めます。
| 組の名前 | 1組の数学のテスト | 2組の数学のテスト |
|---|---|---|
| 母平均 | ||
| 平均 | ||
| 不偏分散 | ||
| サンプルサイズ |
- それぞれのデータの平均値と不偏分散を求めます。
- それぞれのデータから算出される分散をまとめた分散
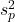 (プールされた分散ともいいます)を、次の式から算出します。
(プールされた分散ともいいます)を、次の式から算出します。 - 次の式から母平均の差
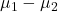 の95%信頼区間を求めます。ただし、「
の95%信頼区間を求めます。ただし、「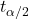 (
(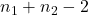 )」は「自由度が(
)」は「自由度が(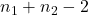 )、信頼係数が
)、信頼係数が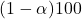 %のときのt分布表の値を示します。
%のときのt分布表の値を示します。
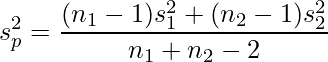
テスト結果のデータに当てはめると、プールした分散は次のようになります。
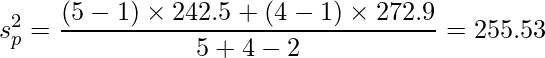
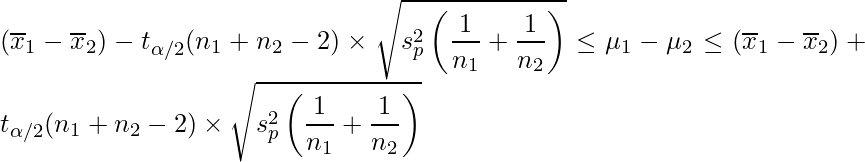
このデータの場合、自由度は5+4-2=7となります。t分布において自由度が7のときの上側2.5%点は「2.365」です。数学のテスト結果のデータを上の式に当てはめると、
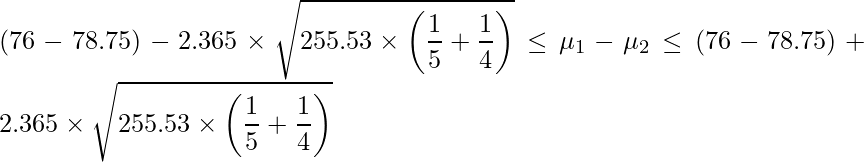
となるので、計算すると次のようになります。
【コラム】母平均の差の検定と正規分布の再生性
正規分布の再生性については14-2章で既に学びました。母集団1と母集団2が母分散の等しい正規分布![]() 、
、![]() に従うとき、これらの母集団から抽出した標本の平均(標本平均)
に従うとき、これらの母集団から抽出した標本の平均(標本平均)![]() 、
、![]() はそれぞれ正規分布
はそれぞれ正規分布![]() 、
、![]() に従うことから、これらの和(差)もまた、正規分布に従います。
に従うことから、これらの和(差)もまた、正規分布に従います。
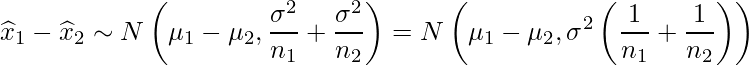
ただし、母分散が既知という状況は一般的にはないので、![]() の代わりに標本から計算した不偏分散
の代わりに標本から計算した不偏分散![]() を使います。2つの標本から2つの不偏分散
を使います。2つの標本から2つの不偏分散![]() 、
、![]() が算出されるので、これらを自由度で重み付けして1つにまとめた分散
が算出されるので、これらを自由度で重み付けして1つにまとめた分散![]() を使います。
を使います。
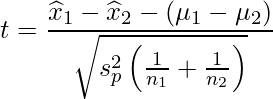
この式から算出されるtの値は自由度![]() のt分布に従います。
のt分布に従います。
■おすすめ書籍
この本は、「こういうことやりたいが、どうしたらよいか?」という方向から書かれています。統計手法をベースに勉強を進めていきたい方はぜひ手にとってみてください。
20. 母平均の区間推定(母分散未知)
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 19. 母平均の区間推定(母分散既知)
19-2. 母平均の信頼区間の求め方(母分散既知)
- 20. 母平均の区間推定(母分散未知)
20-3. 母平均の信頼区間の求め方(母分散未知)
- ブログ
ゴセット、フィッシャー、ネイマン







