- Step1. 基礎編
- 20. 母平均の区間推定(母分散未知)
20-3. 母平均の信頼区間の求め方(母分散未知)
ある工場では、生産している部品Aを1時間毎にランダムに1つ抜き取り、その重さを検査しています。計10個の部品Aの重さを測定した結果、次のようなデータが得られました。ただし、母分散(すべての部品Aの重さから算出した分散)は分かっていません。また、部品Aの重さは正規分布に従うものとします。このデータから母平均の95%信頼区間を求めてみます。
| No. | 部品Aの重さ (g) |
|---|---|
| 1 | 100.2 |
| 2 | 101.5 |
| 3 | 98.0 |
| 4 | 100.1 |
| 5 | 100.9 |
| 6 | 99.6 |
| 7 | 98.6 |
| 8 | 102.1 |
| 9 | 101.4 |
| 10 | 97.9 |
- 標本平均
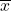 と不偏分散
と不偏分散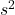 を求める
を求める - 統計量tを計算する
- 2で算出された統計量tがt分布の95%の面積(=確率)の範囲にあればよい(=両端の2.5%の面積の部分の極端な範囲に入らなければよい)ので、t分布表から上側2.5%点を調べる(自由度はn-1=10-1=9)
- 95%信頼区間を求める
抽出した標本の平均値は、![]() =100.03となります。また、不偏分散は次の式より
=100.03となります。また、不偏分散は次の式より![]() =2.22となります。
=2.22となります。
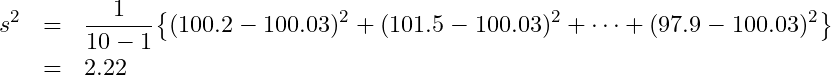
母集団の平均である母平均を![]() 、不偏分散を
、不偏分散を![]() 、抽出したサンプルサイズをnとすると、次の式から統計量tを求められます。
、抽出したサンプルサイズをnとすると、次の式から統計量tを求められます。
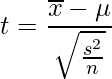
| α | |||||
|---|---|---|---|---|---|
| v | 0.1 | 0.05 | 0.025 | 0.01 | 0.005 |
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 |
| 3 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 |
| 4 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 6 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 |
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 |
| 8 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 |
| 9 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
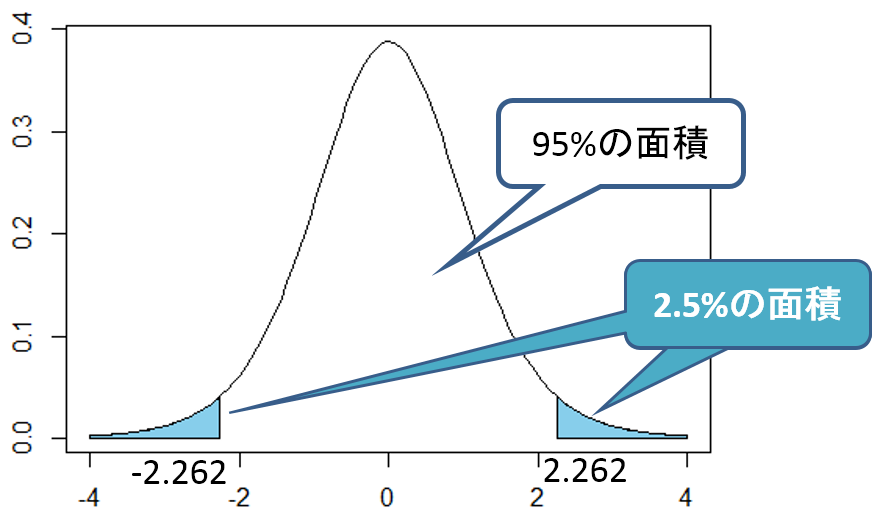
t分布表において上側2.5%点は「2.262」であることから、統計量tの範囲を次のように書けます。
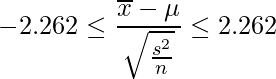
3の式を![]() について変形します。
について変形します。
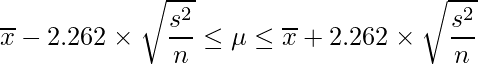
この式を用いることで、母分散が分からない時の母平均μの95%信頼区間を求められます。工場の抜き取り検査のデータに当てはめると、
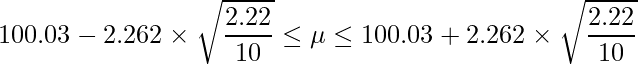
となるので、計算すると次のようになります。
【まとめ】母平均の信頼区間(母分散未知)
母分散が分からない場合、母集団の平均を![]() 、標本平均を
、標本平均を![]() 、不偏分散を
、不偏分散を![]() 、抽出したサンプルサイズをn、信頼係数を
、抽出したサンプルサイズをn、信頼係数を![]() とすると、次の式から母平均
とすると、次の式から母平均![]() の
の![]() 信頼区間を求めることができる。ただし、「
信頼区間を求めることができる。ただし、「![]() 」は「自由度が
」は「自由度が![]() 」のt分布における上側確率が
」のt分布における上側確率が![]() となる値(t値)を示す。
となる値(t値)を示す。
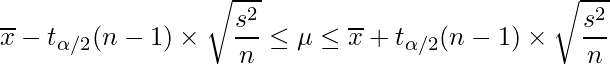
20. 母平均の区間推定(母分散未知)
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
母平均の区間推定(母分散未知)
- 19. 母平均の区間推定(母分散既知)
19-2. 母平均の信頼区間の求め方(母分散既知)
- ブログ
ゴセット、フィッシャー、ネイマン







