- Step1. 基礎編
- 20. 母平均の区間推定(母分散未知)
20-5. さまざまな信頼区間(母分散未知)
19‐4章では、母分散が分かっている場合の母平均の信頼区間において次のことを確認しました。
母分散が分からない場合の母平均の区間推定でも、同様のことを確認してみます。
ある工場では、生産している部品Aを1時間毎に1つ抜き取り、その重さを検査しています。計10個の部品Aの重さを測定した結果、次のようなデータが得られました。このデータを用いて、信頼係数とサンプルサイズを変化させた場合の信頼区間を比較してみます。
| No. | 部品Aの重さ (g) |
|---|---|
| 1 | 100.2 |
| 2 | 101.5 |
| 3 | 98.0 |
| 4 | 100.1 |
| 5 | 100.9 |
| 6 | 99.6 |
| 7 | 98.6 |
| 8 | 102.1 |
| 9 | 101.4 |
| 10 | 97.9 |
| 平均 | 100.03 |
| 不偏分散 | 2.22 |
■信頼係数による信頼区間
- 信頼係数90%のとき
- 信頼係数95%のとき
- 信頼係数99%のとき
t分布において自由度が9のときの上側5%点は「1.833」であることから、次のようになります。
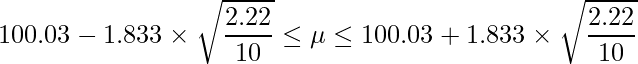
t分布において自由度が9のときの上側2.5%点は「2.262」であることから、次のようになります。
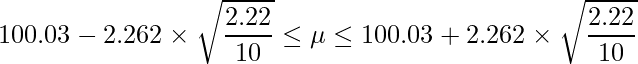
t分布において自由度が9のときの上側0.5%点は「3.25」であることから、次のようになります。
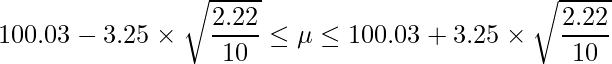
ここまでの結果をまとめると次の表のようになります。この結果から、信頼係数が大きいほど、信頼区間の幅は広くなることが分かります。
| 信頼係数 | 信頼区間 |
|---|---|
| 90% | 99.17 |
| 95% | 98.96 |
| 99% | 98.50 |
■サンプルサイズによる信頼区間
同じデータを用いて、サンプルサイズを変化させた場合の信頼区間も比較してみます。信頼係数は95%とします。
- サンプルサイズが10のとき
- サンプルサイズが20のとき
- サンプルサイズが50のとき
t分布において自由度が10-1=9のときの上側2.5%点は「2.262」であることから、次のようになります。
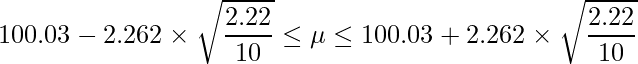
t分布において自由度が20-1=19のときの上側2.5%点は「2.093」であることから、次のようになります。
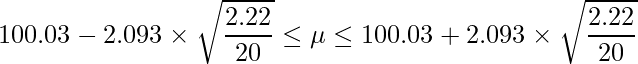
t分布において自由度が50-1=49のときの上側2.5%点は「2.01」であることから、次のようになります。
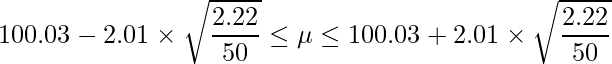
ここまでの結果をまとめると次の表のようになります。この結果から、サンプルサイズnが大きいほど、信頼区間の幅は狭くなることが分かります。
| サンプルサイズ | 信頼区間 |
|---|---|
| 10 | 98.96 |
| 20 | 99.33 |
| 50 | 99.61 |
20. 母平均の区間推定(母分散未知)
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 19. 母平均の区間推定(母分散既知)
19-2. 母平均の信頼区間の求め方(母分散既知)
- 19. 母平均の区間推定(母分散既知)
19-4. さまざまな信頼区間(母分散既知)
- ブログ
ゴセット、フィッシャー、ネイマン







