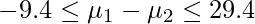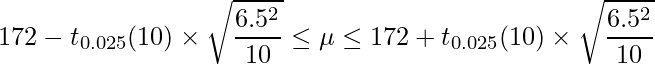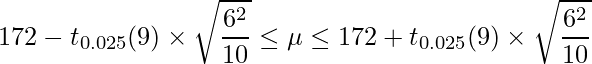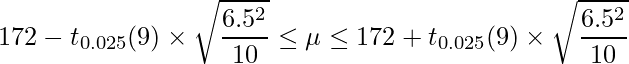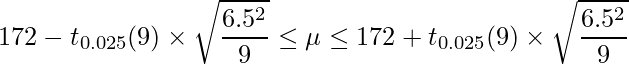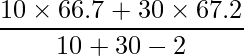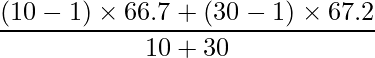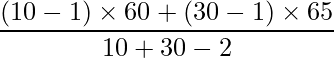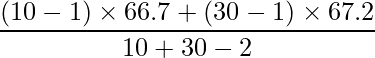- 20. 母平均の区間推定(母分散未知)
練習問題(20. 母平均の区間推定(母分散未知))
1
男性10人をランダムに選んで身長を測定したところ、平均値は172cm、分散は![]() 、不偏分散は
、不偏分散は![]() であった。このとき、男性の平均身長の95%信頼区間を求める式として正しいものを次の1~4の中から選べ。ただし、男性の身長は母分散が未知の正規分布に従うとする。
であった。このとき、男性の平均身長の95%信頼区間を求める式として正しいものを次の1~4の中から選べ。ただし、男性の身長は母分散が未知の正規分布に従うとする。

答えを見る
- 答え
 閉じる
閉じる -
母分散が分からない場合の母平均の信頼区間は、次のようになります。
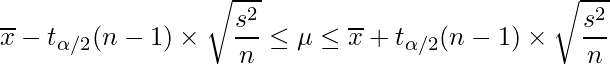
この問題ではサンプルサイズが10で不偏分散は
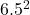 であることから、
であることから、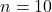 、
、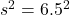 となります。t分布の自由度は10-1=9となることに注意すると、3が正しい答えとなります。
となります。t分布の自由度は10-1=9となることに注意すると、3が正しい答えとなります。ちなみに、
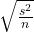 は標本平均の標準誤差SEを表します。標準誤差は「標準偏差s」を「サンプルサイズn」の平方根で割ることで求められます。標準偏差sの計算には不偏分散
は標本平均の標準誤差SEを表します。標準誤差は「標準偏差s」を「サンプルサイズn」の平方根で割ることで求められます。標準偏差sの計算には不偏分散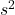 を用いることから、標準誤差は次の式から計算できます。
を用いることから、標準誤差は次の式から計算できます。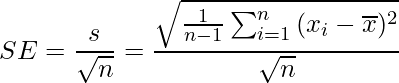
2
男性10人の朝6時と夜22時に身長を測定した合計20個のデータを得た。このとき、朝6時における身長と夜22時における身長の差の平均値の95%信頼区間を求める場合に使用するt分布の自由度を求めよ。ただし、男性の身長は母分散が未知の正規分布に従うとする。

答えを見る
- 答え
 閉じる
閉じる -
このデータは、同じ男性10人に対してそれぞれ朝と夜にデータを測定しているため「対応があるデータ」です。この場合、データとしては20個ありますが、サンプルサイズは10となることに注意すると、使用するt分布の自由度は10-1=9となります。
3
関東地方の男性10人と関西地方の男性30人をサンプリングし、関東と関西の身長の母平均の差の信頼区間を計算したい。二地方の男性の身長の分散と不偏分散が次の表の値で与えられるとき、プールした分散を求める式として正しいものを次の1~4の中から選べ。ただし、それぞれの地方における男性の身長は、母分散は未知であるが等しい正規分布に従うものとする。
| 地方 | 関東地方 | 関西地方 |
|---|---|---|
| 分散 | ||
| 不偏分散 | ||
| サンプルサイズ |

答えを見る
- 答え
 閉じる
閉じる -
プールした分散
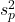 は、次のように求めることができます。
は、次のように求めることができます。
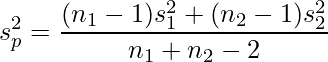
この問題ではサンプルサイズがそれぞれ
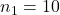 、
、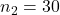 で不偏分散は
で不偏分散は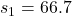 、
、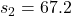 であることから、4が正しい答えとなります。
であることから、4が正しい答えとなります。
4
ある30人のクラスからランダムに5人選んだときの化学のテストの結果は次のとおりであった。このとき、クラス全体の平均点の95%信頼区間を求めよ。ただし、化学のテストの点数は母分散が未知の正規分布に従うとする。
データ:80 95 60 70 100

答えを見る
- 答え
 閉じる
閉じる -
母分散が分からない場合の母平均の95%信頼区間は、次のようになります。
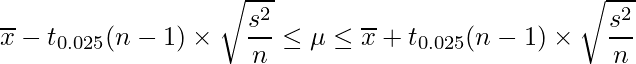
データから計算すると平均は
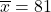 、不偏分散は
、不偏分散は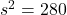 となります。データのサンプルサイズは5であることから、使用するt分布の自由度は5-1=4となります。t分布表を見ると「
となります。データのサンプルサイズは5であることから、使用するt分布の自由度は5-1=4となります。t分布表を見ると「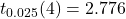 」です。したがって、求める95%信頼区間は次のように計算できます。
」です。したがって、求める95%信頼区間は次のように計算できます。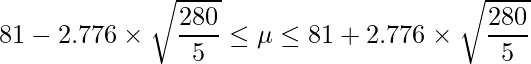
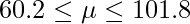
5
A高校の1年生からランダムに6人選んだときの世界史のテスト結果は次のとおりであった。
平均点:80点、不偏分散:300
また、別のB高校の1年生からランダムに8人選んだときの世界史のテスト結果は次のとおりであった。
平均点:70点、不偏分散:250
このとき、A高校とB高校の世界史のテストの平均点の差の95%信頼区間を求めよ。ただし、それぞれの高校における世界史の点数は、母分散は未知であるが等しい正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
まずプールした分散
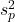 を求めます。
を求めます。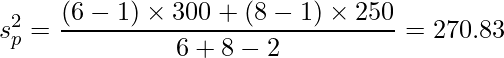
このデータで用いるt分布の自由度は6+8-2=12になります。t分布において自由度が12のときの上側2.5%点は「2.179」です。したがって、数学のテスト結果から平均点の差の95%信頼区間を求めると次のようになります。
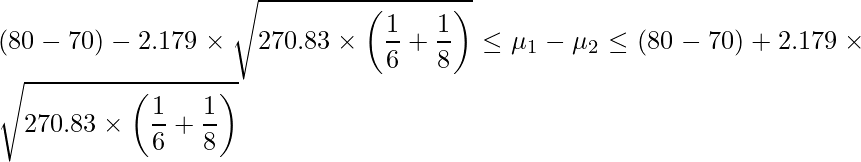
となるので、計算すると次のようになります。