- Step1. 基礎編
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
母平均の推定と同じように、母比率についても区間推定を行うことができます。成功確率が![]() である試行をn回行うときに成功する回数を
である試行をn回行うときに成功する回数を![]() とすると、
とすると、![]() は二項分布
は二項分布![]() に従うことは13-1章で既に学びました。この
に従うことは13-1章で既に学びました。この![]() が母比率に対応します。
が母比率に対応します。
また、二項分布に従う確率変数![]() の期待値と分散はそれぞれ次のようになることは13-2章で既に学びました。
の期待値と分散はそれぞれ次のようになることは13-2章で既に学びました。
nがある程度大きい時は、中心極限定理によって、![]() は正規分布
は正規分布![]() に近似できます。これにより、
に近似できます。これにより、![]() が二項分布
が二項分布![]() に従う場合、
に従う場合、![]() を標準化した値
を標準化した値![]() はnが十分に大きいときには標準正規分布
はnが十分に大きいときには標準正規分布![]() に従います。
に従います。
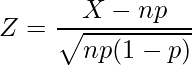
一方、標本比率 ![]() は、
は、![]() (成功回数を試行回数で割ったもの)から求められます。そこで、上の式の分母と分子をnで割り、
(成功回数を試行回数で割ったもの)から求められます。そこで、上の式の分母と分子をnで割り、![]() を
を![]() おくと、次のように変形できます。
おくと、次のように変形できます。
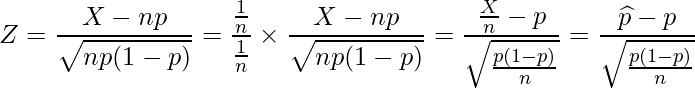
すなわち、次の式もnが十分に大きいとき標準正規分布![]() に従います。また、
に従います。また、![]() は近似的に正規分布
は近似的に正規分布![]() に従います。
に従います。
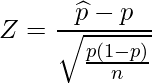
この統計量![]() が標準正規分布
が標準正規分布![]() に従うことを利用して、平均値の区間推定と同様に
に従うことを利用して、平均値の区間推定と同様に![]() についての信頼区間を計算できます。
についての信頼区間を計算できます。
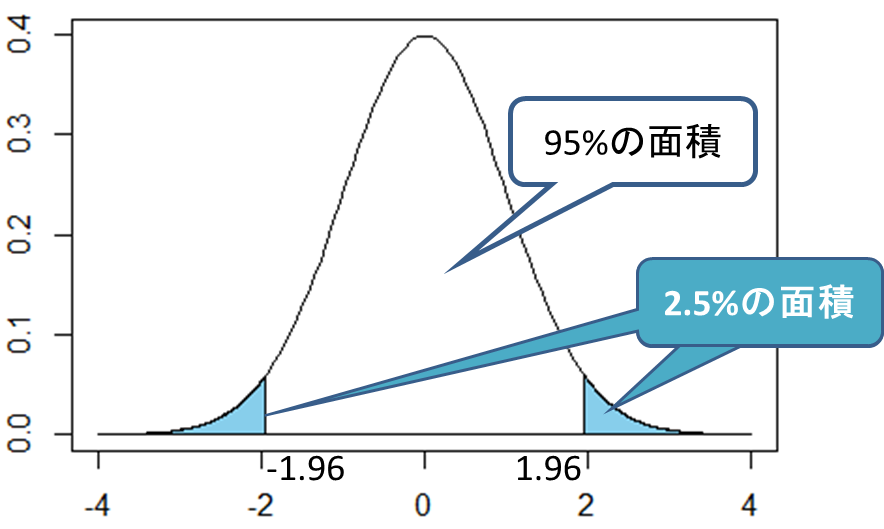
標準正規分布表から読み取った![]() の95%信頼区間は
の95%信頼区間は![]() であることから、
であることから、![]() の式を代入します。
の式を代入します。
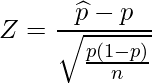
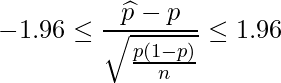
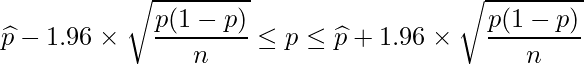
これで母比率![]() についての95%信頼区間を算出するための式が得られました。しかし、この
についての95%信頼区間を算出するための式が得られました。しかし、この![]() の信頼区間の不等式の上限値と下限値には母比率
の信頼区間の不等式の上限値と下限値には母比率![]() が含まれたままなので、信頼区間を計算できません。ここで、
が含まれたままなので、信頼区間を計算できません。ここで、![]() はpの一致推定量であり、nが大きい時にはほぼ
はpの一致推定量であり、nが大きい時にはほぼ![]() に一致すると考えられることから、
に一致すると考えられることから、![]() のpを
のpを![]() で置き換えます。
で置き換えます。
以上をまとめると、母比率![]() の95%信頼区間は次の式から求められます。
の95%信頼区間は次の式から求められます。
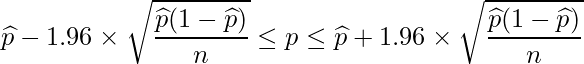
【まとめ】母比率の信頼区間
抽出したサンプルサイズをn、標本比率を![]() 、信頼係数を
、信頼係数を![]() とすると、次の式から母比率
とすると、次の式から母比率![]() の
の![]() 信頼区間を求めることができる。ただし、
信頼区間を求めることができる。ただし、![]() は標準正規分布における上側確率が
は標準正規分布における上側確率が![]() となる値(z値)を表す。
となる値(z値)を表す。
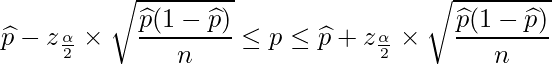
■おすすめ書籍
近年の統計的検定においては、P値だけでなく「効果量」や「信頼区間」、「検出力」にも着目しようという動きが少しずつ広がってきています。今後このような指標がますます重要になってくるはずです。統計解析を行う方は一度読んでおかれることを強くおすすめします。
21. 母比率の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 13. いろいろな確率分布1
13-1. 二項分布
- 13. いろいろな確率分布1
13-2. 二項分布の期待値と分散
- 18. 母平均の点推定
18-3. 推定量の性質
- ブログ
比率が0%のときの信頼区間(3の法則)








