- Step1. 基礎編
- 21. 母比率の区間推定
21-5. 必要なサンプルサイズ2
例題:
ある比率を調査し、95%信頼区間を推定します。信頼区間の幅を4%に収めたい場合、どの程度のサンプルサイズを確保すればよいでしょうか。
母比率![]() の信頼区間の幅が次の式で計算できることは21-4章で既に学びました。
の信頼区間の幅が次の式で計算できることは21-4章で既に学びました。
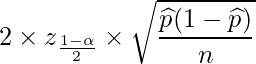
この値が4%(=0.04)以下であればいいので、次の関係が成り立てばよいわけです。
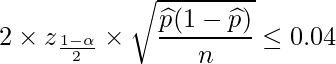
95%信頼区間の場合の![]() は1.96ですが、
は1.96ですが、![]() の値は問題文からは分かりません。このような場合は
の値は問題文からは分かりません。このような場合は![]() =0.5を使います。信頼区間の幅が最も大きくなるのは
=0.5を使います。信頼区間の幅が最も大きくなるのは![]() =0.5の場合であり、
=0.5の場合であり、![]() =0.5の場合について考えておけば、実際の
=0.5の場合について考えておけば、実際の![]() がどのような数値であったとしても、それより信頼区間の幅が大きくなることはないためです。
がどのような数値であったとしても、それより信頼区間の幅が大きくなることはないためです。![]() =0.5を式に代入すると、
=0.5を式に代入すると、
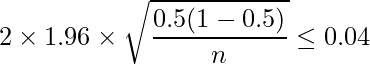
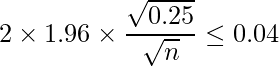
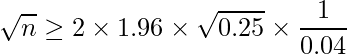
となり、サンプルサイズを2401以上確保すればよいということが分かります。
【コラム】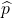 が0.5ではない場合の必要サンプルサイズ
が0.5ではない場合の必要サンプルサイズ
![]() =0.5ではない場合に、95%信頼区間の幅を4%に収めるための必要サンプルサイズは次のようになります。
=0.5ではない場合に、95%信頼区間の幅を4%に収めるための必要サンプルサイズは次のようになります。
| 必要サンプルサイズn | |
|---|---|
| 0 | |
| 0.1 | |
| 0.3 | |
| 0.7 | |
| 0.99 |
21. 母比率の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
母比率の区間推定(無限母集団)
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
- ブログ
sample, population, universe
- ブログ
幾つデータが必要か?






