- Step1. 基礎編
- 21. 母比率の区間推定
21-2. 母比率の信頼区間の求め方2
例題1:
テレビ番組の視聴に関する街頭アンケートを行いました。100人にアンケートを行った結果、A番組を見ている人は10%でした。A番組の視聴率の95%信頼区間はいくらでしょうか。
| A番組を見た | A番組を見ていない | |
|---|---|---|
| 人数 | 10人 | 90人 |
| 割合 | 10% | 90% |
この問題ではサンプルサイズは100人なので、n=100です。また、A番組の視聴率![]() の推定値
の推定値![]() は、
は、![]() =10%=0.1となります。これらの値を区間推定の式に代入します。
=10%=0.1となります。これらの値を区間推定の式に代入します。
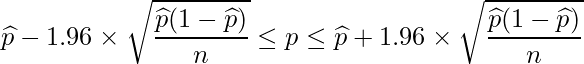
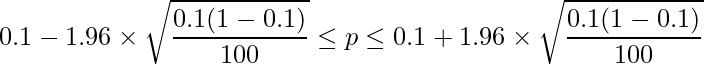
以上の計算から、A番組の視聴率![]() の95%信頼区間は4.1%から15.9%であると求められました。ちなみに、A番組を見ていない人の割合
の95%信頼区間は4.1%から15.9%であると求められました。ちなみに、A番組を見ていない人の割合![]() の95%信頼区間は次のように求められます。
の95%信頼区間は次のように求められます。![]() =90%=0.9です。
=90%=0.9です。
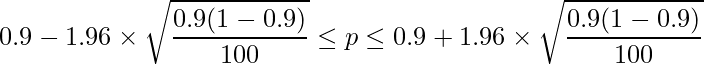
この式から分かるように「A番組の視聴率![]() の95%信頼区間の幅」と「A番組を見ていない人の割合
の95%信頼区間の幅」と「A番組を見ていない人の割合![]() の信頼区間の幅」は等しくなります。
の信頼区間の幅」は等しくなります。
例題2:
無作為に抽出した男性400人に対して新製品のお菓子を食べてもらい、「おいしかった」か「おいしくなかった」かのいずれかを回答してもらいました。その結果、100人が「おいしかった」と回答しました。全国の男性のうち、このお菓子を「おいしい」と評価する割合の95%信頼区間はいくらでしょうか。
| おいしかった | おいしくなかった | |
|---|---|---|
| 人数 | 100人 | 300人 |
| 割合 | 25% | 75% |
この問題ではサンプルサイズは400人なので、n=400です。また、100人が「おいしかった」と評価したので、男性のうちこのお菓子を「おいしい」と評価する割合![]() の推定値
の推定値![]() は、
は、![]() となります。これらの値を区間推定の式に代入します。
となります。これらの値を区間推定の式に代入します。
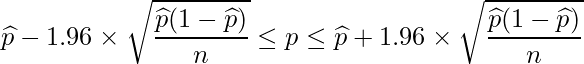
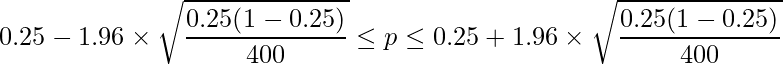
以上の計算から、全国の男性のうち「おいしい」と評価する割合![]() の95%信頼区間は20.8%から29.2%であると求められました。
の95%信頼区間は20.8%から29.2%であると求められました。
21. 母比率の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
母比率の区間推定(無限母集団)
- 13. いろいろな確率分布1
13-1. 二項分布
- 13. いろいろな確率分布1
13-2. 二項分布の期待値と分散
- ブログ
比率が0%のときの信頼区間(3の法則)






