- 21. 母比率の区間推定
練習問題(21. 母比率の区間推定)
1
次の母比率の区間推定についての4つの記述のうち、誤っているものを選べ。
- 母比率の区間推定では、サンプルサイズと点推定値がそれぞれ同じ場合には、95%信頼区間よりも50%信頼区間の方が常に信頼区間の幅は狭くなる。
- 信頼区間の幅を狭くするには、サンプルサイズを増やす以外に方法はない。
- 母比率の信頼区間は、点推定による比率
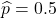 の時に最も広くなる。
の時に最も広くなる。 - サンプルサイズを100倍にすると、信頼区間の幅は
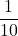 になる。
になる。

答えを見る
- 答え
 閉じる
閉じる -
- ×:正しいです。信頼区間の幅は下式で表すことができます。nと
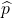 を固定して考えると、これは信頼係数
を固定して考えると、これは信頼係数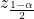 に比例することが分かります。信頼係数は100%に近づくほど大きくなるため、95%信頼区間より50%信頼区間の方が常に幅は狭くなると言えます。
に比例することが分かります。信頼係数は100%に近づくほど大きくなるため、95%信頼区間より50%信頼区間の方が常に幅は狭くなると言えます。
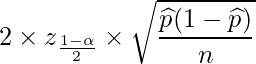
- ◯:誤りです。信頼区間の幅は「母比率が50%から離れる場合」か、「サンプルサイズが大きい場合」か、「信頼係数が小さい場合」により狭くなります。
- ×:正しいです。信頼区間の幅は、
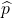 について二次関数となっている部分があります。この部分は、サンプルサイズと信頼係数が固定された場合、
について二次関数となっている部分があります。この部分は、サンプルサイズと信頼係数が固定された場合、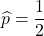 の時に最大値
の時に最大値 を取ります。
を取ります。 - ×:正しいです。信頼区間の幅は、
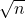 に反比例することが分かります。よって、サンプルサイズが
に反比例することが分かります。よって、サンプルサイズが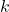 倍になると、信頼区間の幅は
倍になると、信頼区間の幅は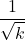 倍となります。
倍となります。
- ×:正しいです。信頼区間の幅は下式で表すことができます。nと
2
サイコロを400回投げたところ、6の目が80回出た。このサイコロで6の目が出る母比率の95%信頼区間を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
母比率の推定値は
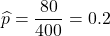 です。これを用いて95%信頼区間を計算すると次のようになります。
です。これを用いて95%信頼区間を計算すると次のようになります。
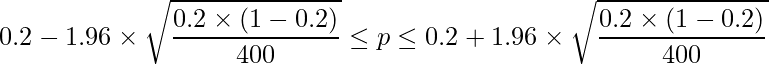
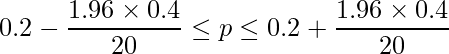
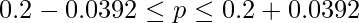
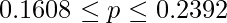
3
ある芸能人の認知度を調べるため街頭アンケートを行ったところ、通行人300人のうち30人がこの芸能人のことを知っていた。信頼係数90%でこの芸能人の認知度の信頼区間を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
母比率の推定値は
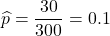 です。これを用いて90%信頼区間を計算すると次のようになります。
です。これを用いて90%信頼区間を計算すると次のようになります。
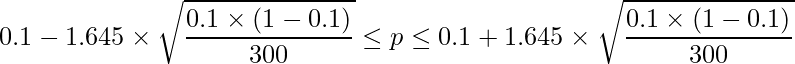
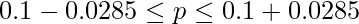
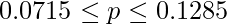
4
ある選挙で立候補者T氏が当選するかどうかをいち早く知るために、出口調査を行うことになった。母比率の95%信頼区間の幅を5%以内にしたい場合、何人以上を対象に調査を行う必要があるか求めよ。ただし、事前調査によりT氏の得票率は60%程度であることが分かっているものとする。

答えを見る
- 答え
 閉じる
閉じる -
母比率の推定値は
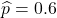 です。これを用いて95%信頼区間の式から次の関係が成り立ちます。
です。これを用いて95%信頼区間の式から次の関係が成り立ちます。
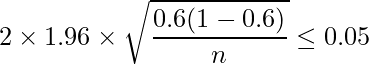
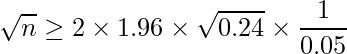
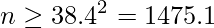
したがって1476人以上に対して出口調査を行えばよいことが分かります。
5
2つのチョコレート菓子TとKについて、どちらが好まれているかを知るためにアンケート調査を行いたい。母比率の95%信頼区間の幅を2%以下に抑えたい場合、最低何人の調査を行う必要があるか求めよ。

答えを見る
- 答え
 閉じる
閉じる -
比率が不明であるので、信頼区間の幅が最大となる
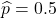 を仮定して信頼区間を計算します。
を仮定して信頼区間を計算します。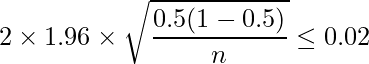
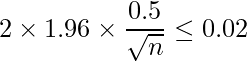
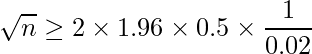
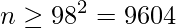
したがって9604人以上に対して調査を行えばよいことが分かります。






