- Step1. 基礎編
- 22. 母分散の区間推定
22-1. カイ二乗分布
カイ二乗分布は、![]() ,
, ![]() , …,
, …, ![]() が互いに独立で標準正規分布
が互いに独立で標準正規分布![]() に従う確率変数であるときに、次の式から算出される自由度
に従う確率変数であるときに、次の式から算出される自由度![]() の
の![]() が従う確率分布のことです。
が従う確率分布のことです。
![]() は「カイ」と読みます。自由度が1のとき、カイ二乗分布は標準正規分布に従う確率変数を二乗したものに等しくなります。
は「カイ」と読みます。自由度が1のとき、カイ二乗分布は標準正規分布に従う確率変数を二乗したものに等しくなります。
自由度が![]() のとき、カイ二乗分布の確率密度関数は次の式で表すことができます。
のとき、カイ二乗分布の確率密度関数は次の式で表すことができます。![]() ()はガンマ関数を表します。カイ二乗分布の式は非常に複雑ですが、覚える必要はありません。
()はガンマ関数を表します。カイ二乗分布の式は非常に複雑ですが、覚える必要はありません。
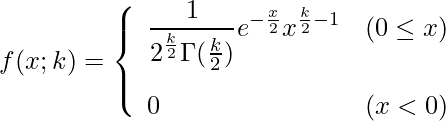
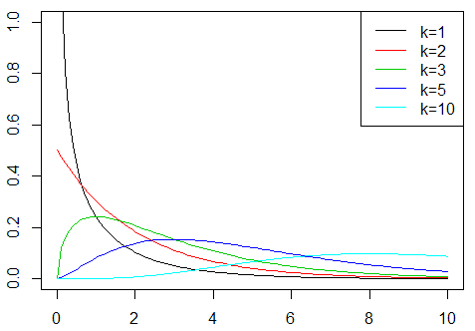
カイ二乗分布は「母分散の区間推定(22-3章)」や「適合度の検定(25‐4章)」、「独立性の検定(25-5章)」を行う際に使われます。カイ二乗分布はt分布と同様、自由度によって形が異なる分布です。自由度を変化させた時のカイ二乗分布の形を見てみます。次のグラフは自由度(グラフ中ではdfで表示しています)が1, 2, 3, 5, 10である場合のカイ二乗分布(黒、赤、緑、青、水色線)です。
■カイ二乗分布の性質
- 期待値と分散
確率変数
 が自由度
が自由度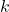 のカイ二乗分布に従っている時、
のカイ二乗分布に従っている時、 の期待値
の期待値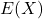 と分散
と分散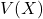 は次のようになります。
は次のようになります。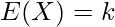
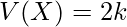
- 再生性
2つの確率変数
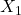 ,
, 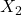 がそれぞれ独立に自由度
がそれぞれ独立に自由度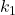 ,
, 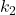 のカイ二乗分布
のカイ二乗分布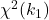 ,
, 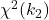 に従うとき、
に従うとき、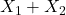 は自由度
は自由度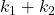 のカイ二乗分布
のカイ二乗分布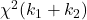 に従います。
に従います。 - 正規分布に従う母集団からの無作為標本
確率変数
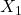 ,
, 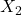 , …,
, …, 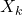 がそれぞれ独立に正規分布
がそれぞれ独立に正規分布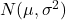 に従うとき、次の式から算出される値は自由度
に従うとき、次の式から算出される値は自由度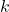 のカイ二乗分布に従います。
のカイ二乗分布に従います。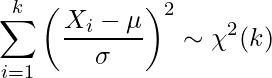
また、この式を展開して得られる次の式の値は自由度
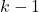 のカイ二乗分布に従います。
のカイ二乗分布に従います。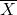 は標本平均を
は標本平均を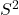 は不偏分散を表します。
は不偏分散を表します。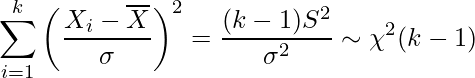
- カイ二乗分布と指数分布の関係
自由度2のカイ二乗分布は
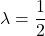 の指数分布と一致します。
の指数分布と一致します。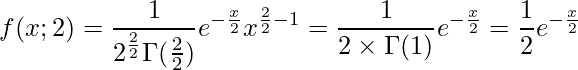
■おすすめ書籍
WEBで公開されているハンバーガー統計学が書籍化したものです。ハンバーガショップの話を軸に進んでいくので、理解しやすいです。
22. 母分散の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 20. 母平均の区間推定(母分散未知)
20-1. 標本とt分布
- ブログ
正規分布, カイ二乗分布, t 分布, F 分布








