- Step1. 基礎編
- 25. さまざまな検定
25-4. 適合度の検定
2つのカテゴリーに属するデータをそれぞれのカテゴリーで同時に分類し、その度数を集計したものをクロス集計表といいます。クロス集計表については5-3章で既に学びました。調査によって得られたクロス集計表がある場合、実測度数がある特定の分布に適合(一致)するかどうかを検定することを適合度の検定といいます。適合度の検定では、カイ二乗分布を用いて検定を行います。
例題:
日本人の血液型の分布はA型が40%、O型が30%、B型が20%、AB型が10%であると言われています。ランダムに選ばれた100人の血液型について次のようなデータが得られた時、このデータは日本人の血液型の分布と同じといえるでしょうか。
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 度数 | 55 | 22 | 16 | 7 | 100 |
日本人の血液型分布と完全に一致していた場合、「理論値」のようになると考えられます。そこで、適合度検定ではこの「理論値」からの「実測値」のズレを算出し、検定を行います。
- 仮説を立てる
- 有意水準を設定する
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説![]() は「調査した血液型分布は日本人の血液型分布と一致する」とします。したがって、対立仮説
は「調査した血液型分布は日本人の血液型分布と一致する」とします。したがって、対立仮説![]() は「調査した血液型分布は日本人の血液型分布と一致しない」となります。
は「調査した血液型分布は日本人の血液型分布と一致しない」となります。
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 実測値 | 55 | 22 | 16 | 7 | 100 |
| 理論値 | 40 | 30 | 20 | 10 | 100 |
![]() とします。
とします。
適合度検定ではカイ二乗分布に従うカイ二乗統計量(=カイ二乗値![]() )使います。カイ二乗値は次のように求めます。
)使います。カイ二乗値は次のように求めます。
①「理論値」からの「実測値」のズレを2乗したものを、「理論値」の値で割る
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 実測値 | 55 | 22 | 16 | 7 | 100 |
| 理論値 | 40 | 30 | 20 | 10 | 100 |
| ズレ | - |
②ズレの和をとる
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 実測値 | 55 | 22 | 16 | 7 | 100 |
| 理論値 | 40 | 30 | 20 | 10 | 100 |
| ズレ | |||||
この結果より、カイ二乗値は![]() =9.458となります。
=9.458となります。
この検定で使用する分布は自由度「4-1=3」の「カイ二乗分布」です。また、適合度検定は上側P値(右側P値)を参照します。統計数値表から![]() の値を読み取ると「7.815」となっています。
の値を読み取ると「7.815」となっています。
| v | 0.99 | 0.975 | 0.95 | 0.9 | 0.1 | 0.05 | 0.025 | 0.01 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.024 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.345 |
| 4 | 0.297 | 0.484 | 0.711 | 1.064 | 7.779 | 9.488 | 11.143 | 13.277 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.070 | 12.833 | 15.086 |
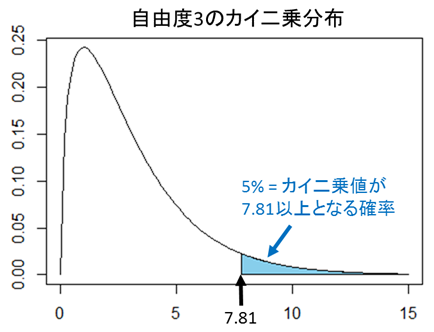
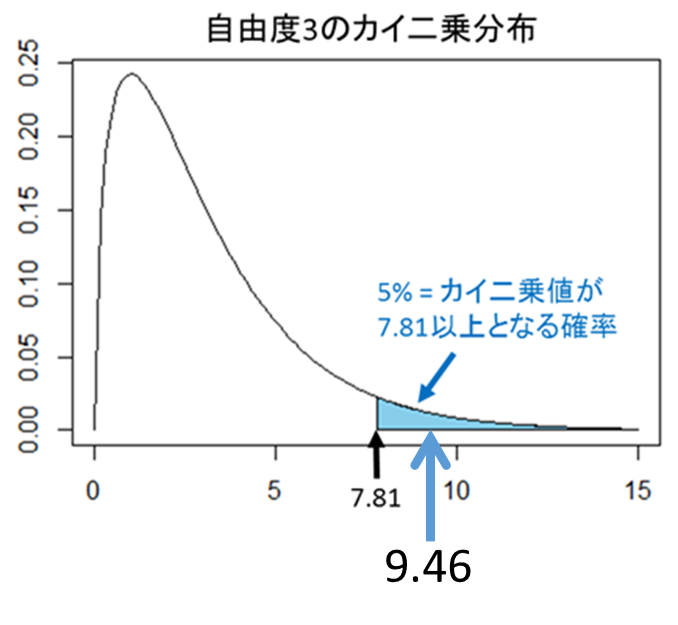
次の図は自由度3のカイ二乗分布を表したものです。![]() =9.458は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり「調査した血液型分布は日本人の血液型分布と一致しない」と結論づけられます。
=9.458は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり「調査した血液型分布は日本人の血液型分布と一致しない」と結論づけられます。
■おすすめ書籍
カテゴリカルデータの分析には様々な手法があります。もっと色々勉強したい方はこちらの本が分かりやすいです。
25. さまざまな検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 22. 母分散の区間推定
22-1. カイ二乗分布
- 22. 母分散の区間推定
22-2. カイ二乗分布表
- ブログ
独立性の検定
- ブログ
クロス集計表から分析する








