- Step1. 基礎編
- 25. さまざまな検定
25-2. 二項分布を用いた検定
25-1章の母比率の検定と同じ問題について、この章では二項分布を用いた検定を行ってみます。
例題:
あるサイコロを12,000回投げたときに1が2,200回出ました。このサイコロはどの目も等しく出る歪みのないサイコロといえるでしょうか。

サイコロを投げて1が出るか、出ないかという試行は2種類の結果しか得られないので、サイコロをn回投げたときに1の目が出る回数![]() は二項分布に従います。
は二項分布に従います。
- 仮説を立てる
- 有意水準を設定する
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説![]() は「このサイコロを12,000回振ったときに1が出るのは2,000回(=12,000/6)である」とします。したがって、対立仮説
は「このサイコロを12,000回振ったときに1が出るのは2,000回(=12,000/6)である」とします。したがって、対立仮説![]() は「このサイコロを12,000回投げたときに1が出るのは2,000回ではない」となります。
は「このサイコロを12,000回投げたときに1が出るのは2,000回ではない」となります。
![]() とします。
とします。
二項分布![]() の場合、
の場合、![]() を確率変数とすると「期待値
を確率変数とすると「期待値![]() 、分散
、分散![]() 」が成り立つことは13-2章で既に学びました。したがって、サンプルサイズnが十分に大きい時には、次の式から得られる統計量zは標準正規分布
」が成り立つことは13-2章で既に学びました。したがって、サンプルサイズnが十分に大きい時には、次の式から得られる統計量zは標準正規分布![]() に従います。ここでは
に従います。ここでは![]() は1が出た回数、
は1が出た回数、![]() は成功確率(=1が出る確率)、nは試行回数を表します。
は成功確率(=1が出る確率)、nは試行回数を表します。
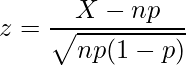
この検定で使用する分布は「標準正規分布」になります。また、サイコロの1の目の出方に歪みがないかどうかを確認したいので、両側検定を行います。統計数値表から![]() の値を読み取ると「1.96」となっています。
の値を読み取ると「1.96」となっています。
試行回数はn=12,000、1が出る確率はp=1/6なので統計量zは次のようになります。
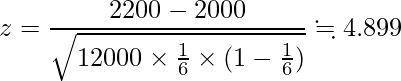
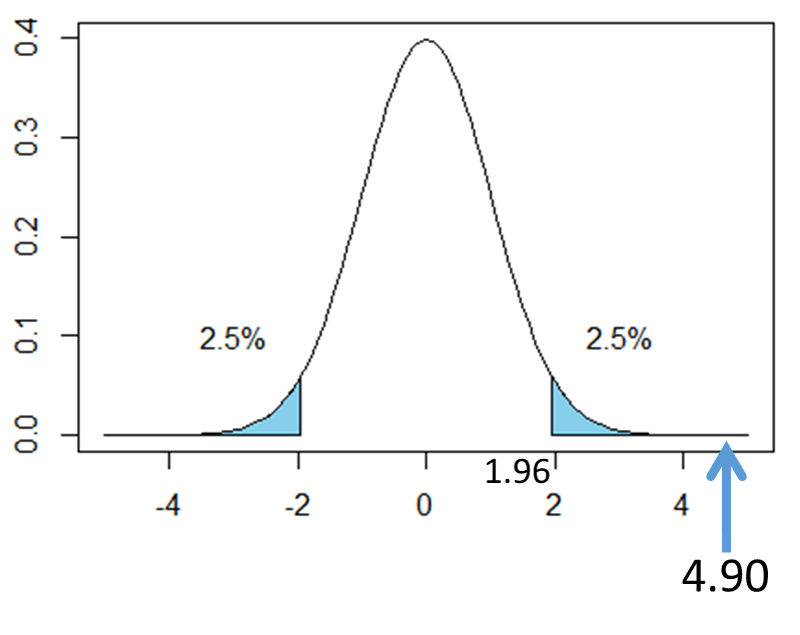
次の図は標準正規分布を表したものです。z=4.899は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり「このサイコロを12,000回投げたときに1が出るのは2,000回ではない、すなわちこのサイコロは1の出やすさに関して歪んでいる」と結論づけられます。
■連続修正
二項分布は離散型確率分布であり、確率変数が取りうる値がとびとびの値です。そのため、連続型確率分布である正規分布に近似しようとすると、誤差が出てしまいます。
例えば、二項分布において確率変数![]() が取りうる値が
が取りうる値が![]() および
および![]() となる確率を考えてみます。これらの確率
となる確率を考えてみます。これらの確率![]() と
と![]() を、二項分布を用いて正規近似により求めようとすると
を、二項分布を用いて正規近似により求めようとすると![]() が1と2の間の値を取る場合の確率は
が1と2の間の値を取る場合の確率は![]() にはすべて含まれるものの、
にはすべて含まれるものの、![]() には全く含まれないことが分かります。
には全く含まれないことが分かります。
これを補正するために行うのが「連続修正」です。具体的には![]() は
は![]() 、
、![]() は
は![]() というように、0.5を使って補正を行います。すなわち、
というように、0.5を使って補正を行います。すなわち、
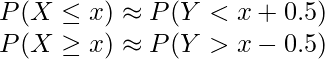
を使って正規近似を行います。(![]() は正規分布に従う確率変数を表します)
は正規分布に従う確率変数を表します)
25. さまざまな検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 13. いろいろな確率分布1
13-1. 二項分布
- 13. いろいろな確率分布1
13-2. 二項分布の期待値と分散
- ブログ
割合と比率
- ブログ
二項検定
- ブログ
2群の比率の差の検定
- ブログ
幾つデータが必要か? - 比率の差の検定






