- Step1. 基礎編
- 25. さまざまな検定
25-3. ポアソン分布を用いた検定
例題:
1ヶ月間に平均20件の自動車事故が起こる見通しの悪いT字路があります。この状況を改善するためにカーブミラーを設置した結果、この1年での事故数は200回になりました。カーブミラーの設置によって、1か月間の平均事故発生頻度は低下したと言えるでしょうか。
事故が起こるという事象は非常に稀な事象なので、1ヶ月で平均![]() 回の事故が起こる場所で、一定時間に事故が起こる回数
回の事故が起こる場所で、一定時間に事故が起こる回数![]() はポアソン分布に従います。
はポアソン分布に従います。
- 仮説を立てる
- 有意水準を設定する
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説![]() は「このT字路では1ヶ月に20回事故が起こる」とします。したがって、対立仮説
は「このT字路では1ヶ月に20回事故が起こる」とします。したがって、対立仮説![]() は「このT字路では1ヶ月に20回事故が起こるとはいえない」となります。
は「このT字路では1ヶ月に20回事故が起こるとはいえない」となります。
![]() とします。
とします。
確率変数![]() がポアソン分布
がポアソン分布![]() に従うとき、「期待値
に従うとき、「期待値![]() =分散
=分散![]() 」が成り立つことは13-4章で既に学びました。この問題では
」が成り立つことは13-4章で既に学びました。この問題では![]() を1年間の事故数、
を1年間の事故数、![]() を各月の事故数とします。問題文より
を各月の事故数とします。問題文より![]() です。ポアソン分布の再生性により
です。ポアソン分布の再生性により![]() はポアソン分布
はポアソン分布![]() に従います。nは調査を行ったポイント数を表します。
に従います。nは調査を行ったポイント数を表します。
また中心極限定理により、サンプルサイズnが十分に大きい時には独立な確率変数の和は正規分布に収束することから、![]() は正規分布
は正規分布![]() に従うと考えることができます。すなわち次の式は標準正規分布N(0,1)に従います。
に従うと考えることができます。すなわち次の式は標準正規分布N(0,1)に従います。
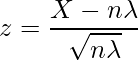
![]() から1か月の事故の数の平均を算出すると、
から1か月の事故の数の平均を算出すると、![]() になります。サンプルサイズnが十分に大きい時には、
になります。サンプルサイズnが十分に大きい時には、![]() は正規分布
は正規分布![]() に従うと考えることができます。このとき次の式から算出される値もまた標準正規分布N(0,1)に従います。
に従うと考えることができます。このとき次の式から算出される値もまた標準正規分布N(0,1)に従います。
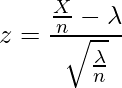
この検定で使用する分布は「標準正規分布」になります。また、事故の発生が改善したか(事故の発生数が20回より少なくなったか)を確認したいので、片側検定を行います。統計数値表から![]() の値を読み取ると「1.645」となっています。
の値を読み取ると「1.645」となっています。
この例題は、1ヶ月単位での平均に対して1年、すなわち12個分のデータを取得した結果なのでn=12となります。1年での事故回数は200回だったことから、1ヶ月単位にすると![]() =200/12=16.67となります。また、
=200/12=16.67となります。また、![]() =20です。これらの値を用いて統計量zを求めます。
=20です。これらの値を用いて統計量zを求めます。
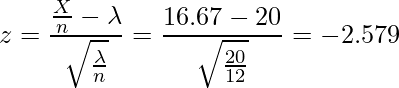
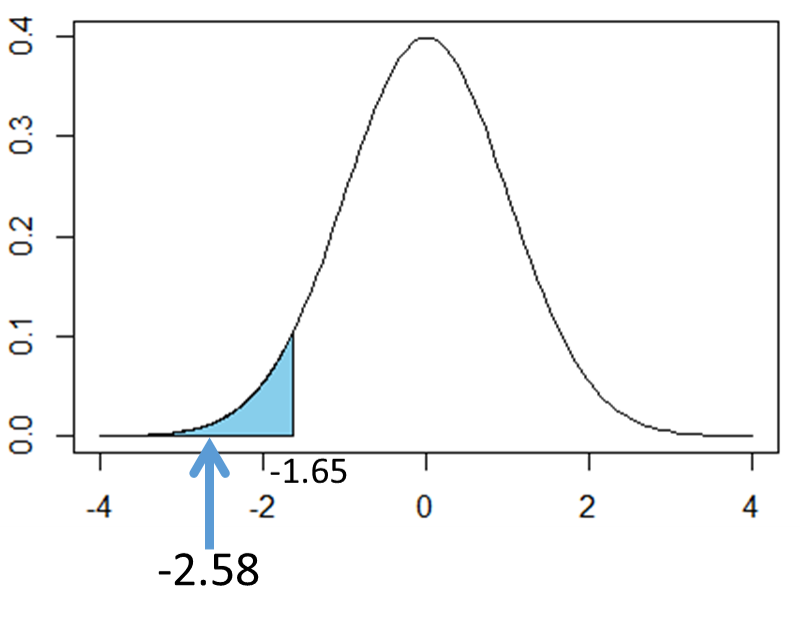
次の図は標準正規分布を表したものです。z=-2.579は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり、「このT字路では1ヶ月に20回事故が起こるとはいえないので、カーブミラーによって自動車事故の発生数は改善された」と結論づけられます。
25. さまざまな検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 13. いろいろな確率分布1
13-3. ポアソン分布
- 13. いろいろな確率分布1
13-4. ポアソン分布の期待値と分散







