- 25. さまざまな検定
練習問題(25. さまざまな検定)
以下の問題でカイ二乗分布表が必要な場合、ページ下部の表を用いてよい。
1
300人に開発中のチョコレート菓子を試食してもらい、おいしいか否かの2択で回答してもらった。その結果、160人が「おいしい」と回答した。このお菓子を「おいしい」と判断する母比率が0.5であるかどうかを有意水準0.05で検定せよ。

答えを見る
- 答え
 閉じる
閉じる -
帰無仮説
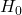 は「母比率
は「母比率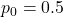 である」となります。標本比率
である」となります。標本比率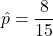 とサンプルサイズn=300を用いて検定統計量zを計算します。
とサンプルサイズn=300を用いて検定統計量zを計算します。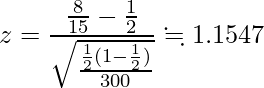
標準正規分布で両端2.5%ずつの範囲になるのは
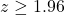 もしくは
もしくは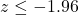 となるときです。問題から算出されたzは1.96より小さいため、「有意水準5%において、帰無仮説
となるときです。問題から算出されたzは1.96より小さいため、「有意水準5%において、帰無仮説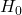 を棄却しない」という結果になります。つまり「母比率は
を棄却しない」という結果になります。つまり「母比率は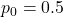 でないとは言えない」と結論づけられます。
でないとは言えない」と結論づけられます。
2
次の表はA県からランダムに300人を集め、年齢区分別人口の割合を集計した結果である。A県の年齢区分別人口割合が、年少人口13%、生産年齢人口58%、老年人口29%であると予想されていたとき、A県の年齢区分別人口割合の予測値の分布と実測値の分布が異なっているかどうかを有意水準0.05で検定せよ。
| 年少人口 | 生産年齢人口 | 老年人口 | 合計 | |
|---|---|---|---|---|
| 予測値 | 39(13%) | 174(58%) | 87(29%) | 300 |
| 実測値 | 44 | 188 | 68 | 300 |

答えを見る
- 答え
 閉じる
閉じる -
帰無仮説
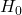 を「年齢区分別人口割合の予測値の分布と実測値の分布は等しい」と設定し、予測値の分布に対する実測値の分布のズレ具合をカイ二乗分布を用いた適合度検定により確かめます。カイ二乗統計量を計算すると次のようになります。
を「年齢区分別人口割合の予測値の分布と実測値の分布は等しい」と設定し、予測値の分布に対する実測値の分布のズレ具合をカイ二乗分布を用いた適合度検定により確かめます。カイ二乗統計量を計算すると次のようになります。年少人口 生産年齢人口 老年人口 合計 予測値 39 174 87 300 実測値 44 188 68 300 ズレ 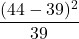
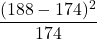
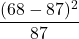
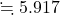
自由度2のカイ二乗分布の右側5%点の値が5.99であることから、「有意水準5%において、帰無仮説
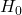 を棄却しない」という結果になります。つまり、「A県における年齢区分別人口割合の実測値の分布は予測値の分布と異なるとは言えない」と結論づけられます。
を棄却しない」という結果になります。つまり、「A県における年齢区分別人口割合の実測値の分布は予測値の分布と異なるとは言えない」と結論づけられます。
3
ランダムに選んだ100人に対して「甘いものが好きか」と「よくお酒を飲むか」の2つの質問をしたところ、次のような結果が得られた。この結果から2つの要素は独立と言えるかどうかを有意水準0.05で検定せよ。
| 甘いものが好き | 好きではない | 合計 | |
|---|---|---|---|
| よくお酒を飲む | 20 | 40 | 60 |
| 飲まない | 30 | 10 | 40 |
| 合計 | 50 | 50 | 100 |

答えを見る
- 答え
 閉じる
閉じる -
カイ二乗分布を用いた独立性の検定を行います。帰無仮説
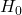 は「2つの好みの関連はない」です。最初に期待度数を計算すると、
は「2つの好みの関連はない」です。最初に期待度数を計算すると、甘いものが好き 好きではない 合計 よくお酒を飲む 30 30 60 飲まない 20 20 40 合計 50 50 100 となります。次に、カイ二乗統計量のためのズレを計算します。
甘いものが好き 好きではない よくお酒を飲む 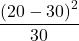
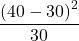
飲まない 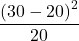
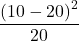
これらを全て足すと16.7となります。この表は2行2列の表であるため、自由度は
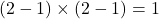 となります。自由度1のカイ二乗分布の右側5%点の値が3.841であることから、「有意水準5%において、帰無仮説
となります。自由度1のカイ二乗分布の右側5%点の値が3.841であることから、「有意水準5%において、帰無仮説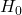 を棄却し、対立仮説
を棄却し、対立仮説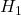 を採択する」という結果になります。つまり「2つの好みの間に関連がある」と結論づけられます。
を採択する」という結果になります。つまり「2つの好みの間に関連がある」と結論づけられます。
4
あるドラマの視聴率が30%だったという記事が、怪しい週刊誌に掲載された。この記事に信憑性があるかどうか確認するため、ランダムに選んだ250人にアンケートを取ったところ55人がそのドラマを見ていたことが分かった。この結果から、週刊誌の記事を信用できるか有意水準0.05で検定せよ。

答えを見る
- 答え
 閉じる
閉じる -
帰無仮説
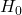 は「視聴率は
は「視聴率は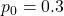 である」となります。標本比率
である」となります。標本比率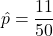 とサンプルサイズn=250を用いて検定統計量zを計算します。
とサンプルサイズn=250を用いて検定統計量zを計算します。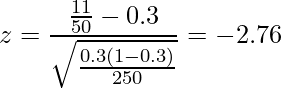
標準正規分布で両端2.5%ずつの範囲になるのは
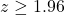 もしくは
もしくは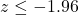 となるときです。問題から算出されたzは-1.96より小さいため、「有意水準5%において、帰無仮説
となるときです。問題から算出されたzは-1.96より小さいため、「有意水準5%において、帰無仮説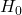 を棄却し、対立仮説
を棄却し、対立仮説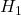 を採択する」という結果になります。つまり「視聴率は30%であるとは言えず、週刊誌の記事(ネタ元?)は怪しい」と結論づけられます。
を採択する」という結果になります。つまり「視聴率は30%であるとは言えず、週刊誌の記事(ネタ元?)は怪しい」と結論づけられます。
5
次の表は、ある小学校の1年生と2年生に好きなスポーツを質問した結果である。この結果から、学年とスポーツの好みに関連があるかどうかを有意水準0.05で検定せよ。
| サッカー | ドッジボール | なわとび | 鬼ごっこ | 合計 | |
|---|---|---|---|---|---|
| 1年生 | 10 | 50 | 25 | 40 | 125 |
| 2年生 | 25 | 65 | 10 | 50 | 150 |
| 合計 | 35 | 115 | 35 | 90 | 275 |

答えを見る
- 答え
 閉じる
閉じる -
カイ二乗分布を用いた独立性の検定を行います。帰無仮説
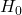 は「学年とスポーツの好みに関連はない(=独立である)」です。
は「学年とスポーツの好みに関連はない(=独立である)」です。カイ二乗値を計算すると13.766となります。この表は2行4列の表であるため、自由度は
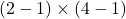 =3となります。自由度3のカイ二乗分布の右側5%点の値が7.815であることから、「有意水準5%において、帰無仮説
=3となります。自由度3のカイ二乗分布の右側5%点の値が7.815であることから、「有意水準5%において、帰無仮説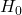 を棄却し、対立仮説
を棄却し、対立仮説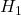 を採択する」という結果になります。つまり「学年とスポーツの好みに関連がある(=独立ではない)」と結論づけられます。
を採択する」という結果になります。つまり「学年とスポーツの好みに関連がある(=独立ではない)」と結論づけられます。
カイ二乗分布表
| v | 0.99 | 0.975 | 0.95 | 0.9 | 0.1 | 0.05 | 0.025 | 0.01 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.024 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.345 |
| 4 | 0.297 | 0.484 | 0.711 | 1.064 | 7.779 | 9.488 | 11.143 | 13.277 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.070 | 12.833 | 15.086 |







