- Step1. 基礎編
- 22. 母分散の区間推定
22-3. 母分散の信頼区間の求め方1
20-3章で学んだ母平均や21-1章で学んだ母比率の推定と同じように、母分散についても区間推定を行うことができます。母分散の区間推定では正規分布やt分布ではなく、カイ二乗分布を使います。
母集団が母分散![]() の正規分布に従う時、抽出された標本のサンプルサイズをn、不偏分散を
の正規分布に従う時、抽出された標本のサンプルサイズをn、不偏分散を![]() とすると、次の式で表される
とすると、次の式で表される![]() (カイ二乗)が自由度
(カイ二乗)が自由度![]() のカイ二乗分布に従うことを用いて母分散の信頼区間を計算します。
のカイ二乗分布に従うことを用いて母分散の信頼区間を計算します。
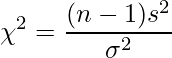
例題:
次の表は、2015年12月末時点の各都道府県内にある映画館のスクリーンの合計数のデータから無作為に10都道府県のデータを抽出したものです。スクリーン数の分布は正規分布に従うものとします。このデータから母分散の95%信頼区間を求めてみます。
| No. | 都道府県 | 全スクリーン数 |
|---|---|---|
| 1 | 兵庫 | 126 |
| 2 | 大阪 | 224 |
| 3 | 奈良 | 34 |
| 4 | 岩手 | 25 |
| 5 | 千葉 | 199 |
| 6 | 茨城 | 89 |
| 7 | 福岡 | 178 |
| 8 | 山梨 | 14 |
| 9 | 滋賀 | 38 |
| 10 | 鳥取 | 11 |
| ― | 平均 | 93.8 |
- 標本の不偏分散を求める
- 使用するカイ二乗分布の自由度を決める
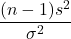 の値(偏差平方和を分散で割った値)がカイ二乗分布の95%の面積(=確率)の範囲にあればいい(=両端の2.5%の面積の部分の極端な範囲に入らなければいい)ので、カイ二乗分布表から自由度9における上側2.5%点と下側2.5%点(=上側97.5%点)を調べる
の値(偏差平方和を分散で割った値)がカイ二乗分布の95%の面積(=確率)の範囲にあればいい(=両端の2.5%の面積の部分の極端な範囲に入らなければいい)ので、カイ二乗分布表から自由度9における上側2.5%点と下側2.5%点(=上側97.5%点)を調べる- 95%信頼区間を求める
抽出した標本の不偏分散を次の式から求めます。
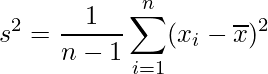
n=10を代入すると次のようになります。
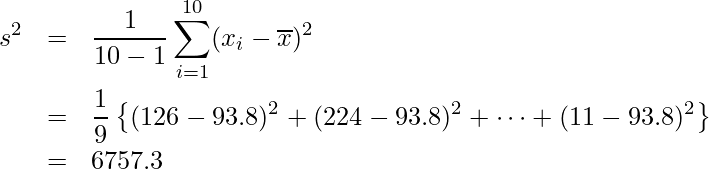
サンプルサイズが10であることから自由度が10-1=9のカイ二乗分布を用います。
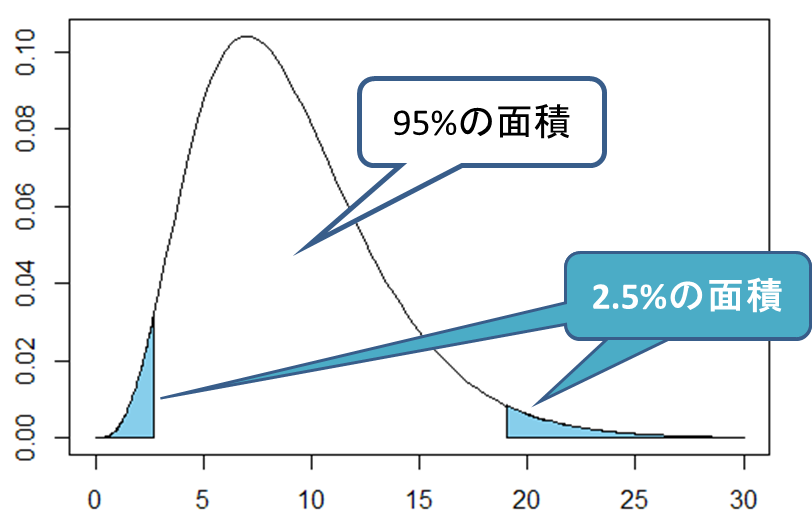
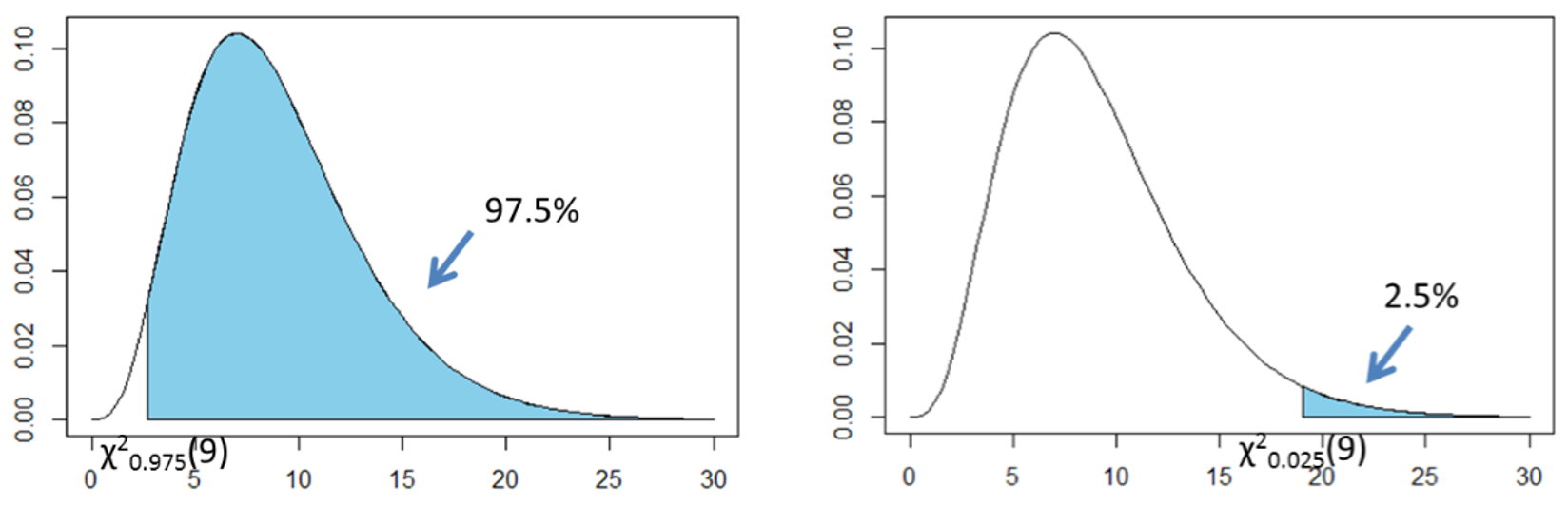
ただし、カイ二乗分布は左右対称ではないので、上側2.5%点と下側2.5%点をそれぞれ読み取る必要があります。次の図のように自由度が9における![]() が0.975の値と0.025の値を読み取ります。
が0.975の値と0.025の値を読み取ります。
| α | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.99 | 0.975 | 0.95 | 0.90 | 0.10 | 0.05 | 0.025 | 0.01 | |
| 1 | 0.00 | 0.00 | 0.00 | 0.02 | 2.71 | 3.84 | 5.02 | 6.64 |
| 2 | 0.02 | 0.05 | 0.10 | 0.21 | 4.61 | 5.99 | 7.38 | 9.21 |
| 3 | 0.12 | 0.22 | 0.35 | 0.58 | 6.25 | 7.82 | 9.35 | 11.35 |
| 4 | 0.30 | 0.48 | 0.71 | 1.06 | 7.78 | 9.49 | 11.14 | 13.28 |
| 5 | 0.55 | 0.83 | 1.15 | 1.61 | 9.24 | 11.07 | 12.83 | 15.09 |
| 6 | 0.87 | 1.24 | 1.64 | 2.20 | 10.65 | 12.59 | 14.45 | 16.81 |
| 7 | 1.24 | 1.69 | 2.17 | 2.83 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.65 | 2.18 | 2.73 | 3.49 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.09 | 2.70 | 3.33 | 4.17 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.56 | 3.25 | 3.94 | 4.87 | 15.99 | 18.31 | 20.48 | 23.21 |
カイ二乗分布において上側2.5%点は「![]() =19.02」、下側2.5%点は「
=19.02」、下側2.5%点は「![]() =2.70」であることから、
=2.70」であることから、![]() の範囲は次のように書けます。
の範囲は次のように書けます。
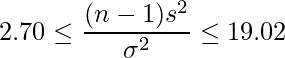
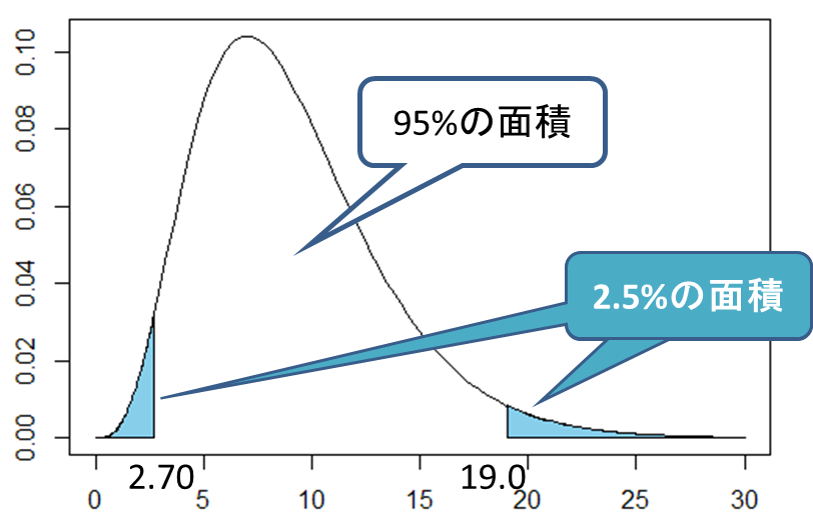
3. の式を書き換えます。
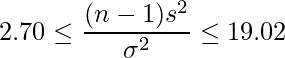
分母と分子を入れ替えます。これにより、不等号の向きが全て逆向きになります。
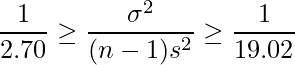
見やすくするため、不等号の向きを全て逆向きに戻します。
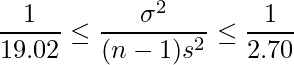
全てに![]() をかけます。
をかけます。![]() は正の数なので、
は正の数なので、![]() をかけても不等号の向きは変わりません。
をかけても不等号の向きは変わりません。
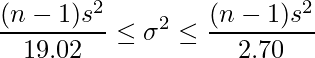
この式を用いることで、母分散![]() の95%信頼区間を求められます。合計スクリーン数のデータに当てはめると、
の95%信頼区間を求められます。合計スクリーン数のデータに当てはめると、
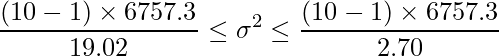
となるので、計算すると
となります。標準偏差![]() の場合の信頼区間は√(ルート)をとることで求められます。
の場合の信頼区間は√(ルート)をとることで求められます。
【まとめ】母分散の信頼区間
サンプルサイズをn、母分散を![]() 、標本から得られた不偏分散を
、標本から得られた不偏分散を![]() 、信頼係数を
、信頼係数を![]() とすると、次の式から母分散
とすると、次の式から母分散![]() の
の![]() 信頼区間を求めることができる。ただし、「
信頼区間を求めることができる。ただし、「![]() 」は「自由度が
」は「自由度が![]() 」のカイ二乗分布における上側確率が
」のカイ二乗分布における上側確率が![]() となる値を、「
となる値を、「![]() 」は下側確率が
」は下側確率が![]() となる値を示す。
となる値を示す。
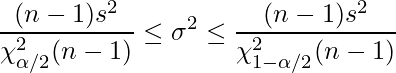
22. 母分散の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 20. 母平均の区間推定(母分散未知)
20-3. 母平均の信頼区間の求め方(母分散未知)
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
- ブログ
正規分布, カイ二乗分布, t 分布, F 分布






