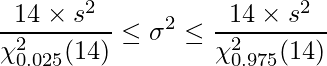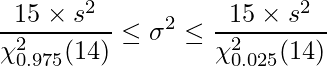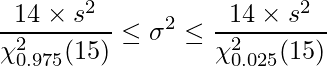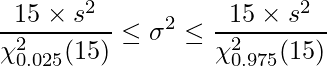- 22. 母分散の区間推定
練習問題(22. 母分散の区間推定)
以下の問題でカイ二乗分布表が必要な場合、ページ下部の表を用いてよい。
1
次の母分散の区間推定、およびカイ二乗分布についての記述のうち、正しいものを選べ。
- 母分散の区間推定で用いる分布は標準正規分布である。
- 自由度が大きくなるにつれてカイ二乗分布は正規分布に近づく。
- カイ二乗分布表を読み取る際には、自由度が2つ必要である。
- カイ二乗分布は左右対称である。

答えを見る
- 答え
 閉じる
閉じる -
- ×:母分散の区間推定で用いる分布はカイ二乗分布です。
- ◯:正しいです。自由度が大きくなると、カイ二乗分布は正規分布に近づきます。ただし、近づき方はとてもゆっくりしています。
- ×:カイ二乗分布を読む際に必要なのは1つの自由度のみです。2つの自由度が必要なのはF分布です。
- ×:カイ二乗分布は正規分布やt分布と異なり左右対称ではありません。
2
ある会社で残業時間を集計することになった。社内からランダムに選ばれた15人の残業時間を計算すると、1日あたりの平均残業時間は2.3時間(不偏分散0.3)であった。このとき、母分散の95%信頼区間を求める式として正しいものはどれか。ただし、残業時間の分布は正規分布に従うものとします。

答えを見る
- 答え
 閉じる
閉じる -
95%信頼区間は下の式から求めます。ただし、nはサンプルサイズを、
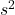 は標本から得られた不偏分散を、
は標本から得られた不偏分散を、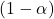 (=
(=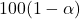 %)は信頼係数を表します。したがって正しい式は「1」となります。
%)は信頼係数を表します。したがって正しい式は「1」となります。
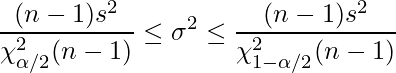
3
あるメーカーが生産している自動車Aの10台の燃費を計測したところ、その不偏分散は![]() であった。この自動車Aの燃費の母分散の95%信頼区間を求めよ。
であった。この自動車Aの燃費の母分散の95%信頼区間を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
10台の自動車からのデータであるので、自由度9のカイ二乗分布を用います。自由度9のカイ二乗分布の上側97.5%点と2.5%点の値はそれぞれ2.70、19.02であることから、母分散の信頼区間は下記のようにして求められます。
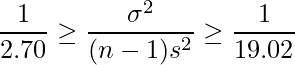
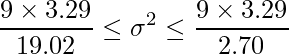
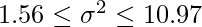
4
男性9人をランダムに選び、40秒間での腕立て伏せの回数を記録した。男性の腕立て伏せの回数の母分散の90%信頼区間を求めよ。
| No. | 記録 |
|---|---|
| 1 | 24 |
| 2 | 28 |
| 3 | 22 |
| 4 | 31 |
| 5 | 28 |
| 6 | 25 |
| 7 | 27 |
| 8 | 26 |
| 9 | 25 |

答えを見る
- 答え
 閉じる
閉じる -
不偏分散を求めると6.94となります。9人からのデータであるので、自由度8のカイ二乗分布を用います。90%信頼区間を求める問題であるため、5%点と95%点の値が必要となることに注意してください。自由度8のカイ二乗分布の上側95%点と5%点の値はそれぞれ2.73、15.51であることから、母分散の信頼区間は下記のようにして求められます。
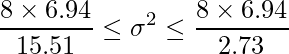
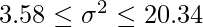
5
ランダムに選んだ男性5人の身長を測定したところ、次のようなデータが得られた。男性の身長の母分散の95%信頼区間を求めよ。
| No. | 身長[cm] |
|---|---|
| 1 | 175.8 |
| 2 | 171.9 |
| 3 | 172.7 |
| 4 | 170.3 |
| 5 | 180.2 |

答えを見る
- 答え
 閉じる
閉じる -
不偏分散を求めると15.33となります。5人からのデータであるので、自由度4のカイ二乗分布を用います。自由度4のカイ二乗分布の上側97.5%点と2.5%点の値はそれぞれ0.48、11.14であることから、母分散の信頼区間は下記のようにして求められます。
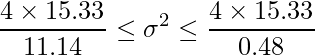
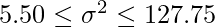
カイ二乗分布表
| α | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.99 | 0.975 | 0.95 | 0.90 | 0.10 | 0.05 | 0.025 | 0.01 | |
| 1 | 0.00 | 0.00 | 0.00 | 0.02 | 2.71 | 3.84 | 5.02 | 6.64 |
| 2 | 0.02 | 0.05 | 0.10 | 0.21 | 4.61 | 5.99 | 7.38 | 9.21 |
| 3 | 0.12 | 0.22 | 0.35 | 0.58 | 6.25 | 7.82 | 9.35 | 11.35 |
| 4 | 0.30 | 0.48 | 0.71 | 1.06 | 7.78 | 9.49 | 11.14 | 13.28 | 5 | 0.55 | 0.83 | 1.15 | 1.61 | 9.24 | 11.07 | 12.83 | 15.09 |
| 6 | 0.87 | 1.24 | 1.64 | 2.20 | 10.65 | 12.59 | 14.45 | 16.81 |
| 7 | 1.24 | 1.69 | 2.17 | 2.83 | 12.02 | 14.07 | 16.01 | 18.48 |
| 8 | 1.65 | 2.18 | 2.73 | 3.49 | 13.36 | 15.51 | 17.54 | 20.09 |
| 9 | 2.09 | 2.70 | 3.33 | 4.17 | 14.68 | 16.92 | 19.02 | 21.67 |
| 10 | 2.56 | 3.25 | 3.94 | 4.87 | 15.99 | 18.31 | 20.48 | 23.21 |