- Step1. 基礎編
- 22. 母分散の区間推定
22-4. 母分散の信頼区間の求め方2
例題:
ある工場で生産される部品Aを10個無作為抽出し、寸法を測定しました。測定した寸法から不偏分散![]() を求めると2.5になりました。このとき母分散の95%信頼区間はいくらでしょうか。ただし部品の寸法は正規分布に従うものとします。
を求めると2.5になりました。このとき母分散の95%信頼区間はいくらでしょうか。ただし部品の寸法は正規分布に従うものとします。
この問題ではサンプルサイズは10なので、n=10です。したがって、自由度10-1=9のカイ二乗分布を使います。自由度9のカイ二乗分布において上側2.5%点は「![]() 」、下側2.5%点は「
」、下側2.5%点は「![]() 」であることから、これらの値を母分散の区間推定の式に代入します。
」であることから、これらの値を母分散の区間推定の式に代入します。
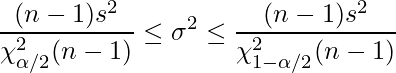
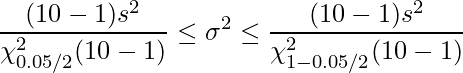
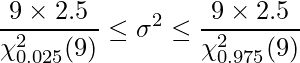
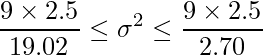
以上の計算から、部品Aの母分散![]() の95%信頼区間は1.18から8.33であると求められました。
の95%信頼区間は1.18から8.33であると求められました。
母分散の信頼区間を求める上での注意点は次の2点です。
- 分子は「サンプルサイズn-1」に不偏分散をかけたものです。「サンプルサイズn」に不偏分散をかけたものではありません。
- 次の図を見ると、
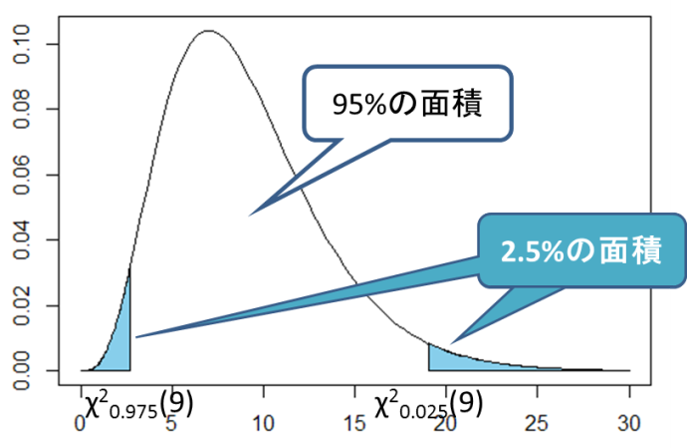
母分散![]() の95%信頼区間の式を
の95%信頼区間の式を
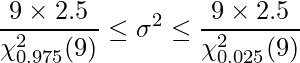
と書いてしまいそうになりますがこれは間違いです。正しくは次のようになります。分母に注意してください。
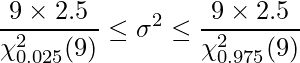
22. 母分散の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 20. 母平均の区間推定(母分散未知)
20-3. 母平均の信頼区間の求め方(母分散未知)
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
- ブログ
正規分布, カイ二乗分布, t 分布, F 分布






