- Step1. 基礎編
- 21. 母比率の区間推定
21-6. 母比率の差の信頼区間
21-1章および21-2章では母比率の信頼区間の求め方について学びました。この章では、2つの標本から得た標本比率を使って母比率の差の信頼区間を算出する方法について学びます。
例題:
ある新製品の野菜ジュースについてアンケート調査を行ったところ、女性では200人中80人が、男性では300人中60人が買ってみたいと答えました。この結果から、この野菜ジュースを買ってみたいと答えた割合の差の95%信頼区間はいくらでしょうか。
| 女性 | 男性 | |
|---|---|---|
| 調査人数 | 200 | 300 |
| 買ってみたいと答えた人数 | 80 | 60 |
| 買ってみたいと答えた割合 | 0.4 | 0.2 |
正規分布の再生性については14-2章で既に学びました。確率変数 ![]() が二項分布
が二項分布 ![]() に従うとき、
に従うとき、![]() が十分に大きい場合には
が十分に大きい場合には ![]() は近似的に正規分布
は近似的に正規分布 ![]() に従うので(21-1章)、これらの和もまた正規分布に従います。ただし、1群目の標本比率を
に従うので(21-1章)、これらの和もまた正規分布に従います。ただし、1群目の標本比率を ![]() 、サンプルサイズを
、サンプルサイズを ![]() 、2群目の標本比率を
、2群目の標本比率を ![]() 、サンプルサイズを
、サンプルサイズを ![]() とします。
とします。
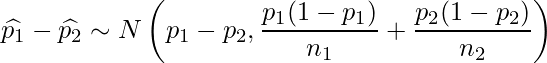
この式を変形すると、
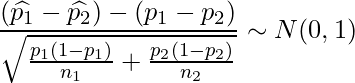
となり、![]() が十分に大きい場合には
が十分に大きい場合には 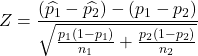 は標準正規分布
は標準正規分布 ![]() に従います。
に従います。
この統計量 ![]() が標準正規分布
が標準正規分布 ![]() に従うことを利用すると、信頼係数を
に従うことを利用すると、信頼係数を ![]() としたときの母比率の差の
としたときの母比率の差の ![]() 信頼区間は次のようになります。ただし、
信頼区間は次のようになります。ただし、![]() は標準正規分布における上側確率が
は標準正規分布における上側確率が![]() となる値(z値)を表します。
となる値(z値)を表します。
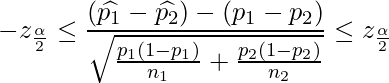
この式を展開することで、
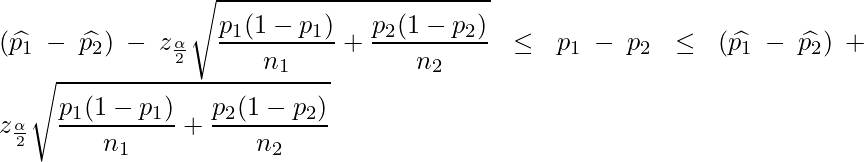
となります。ここで、![]() は
は ![]() の一致推定量であり、
の一致推定量であり、![]() が大きい時にはほぼ
が大きい時にはほぼ ![]() に一致すると考えられることから、
に一致すると考えられることから、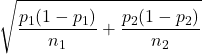 の
の ![]() を
を ![]() で置き換えると、次のようになります。
で置き換えると、次のようになります。
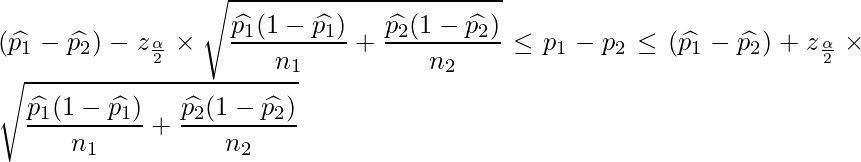
問題より、女性では![]() 、
、![]() 、男性では
、男性では![]() 、
、![]() です。したがって、これらを代入すると求める95%信頼区間は、
です。したがって、これらを代入すると求める95%信頼区間は、
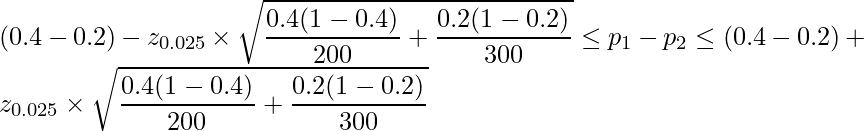
となります。






