幾つデータが必要か？―平均値の差の検定

ブログ

2017/08/19

※コラム「統計備忘録」の記事一覧はこちら※

t検定で有意差検定を行う場合、2群間で僅かでも差があるなら、データの個数をどんどん増やしさえすれば、理論的にはいつか有意になります。しかしながら、予算にも時間にも限りがありますし、動物実験でそんなことをしたら倫理的にも許されないですね。それでは幾つデータを採ればよいのでしょうか。

統計Tipsでは区間推定の場合に必要なサンプルサイズを計算することができますが、ここでは、t検定の場合の簡単な必要サンプルサイズ ( n ) の計算方法を紹介します。この方法は『論文が読める！早分かり統計学』という本に紹介されていたものです。

created by Rinker

¥4,290 (2024/11/21 10:21:08時点 Amazon調べ-詳細)

式はたったのこれだけです。

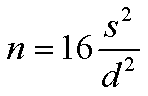
この式は、有意水準を5%としたときに、対立仮説が正しいときは80%の検出力で有意判定を行えるよう n を求めています。式中の s² の s は標準偏差です。先行研究を調べるか予備実験をすれば標準偏差の値を決められると思います。d² の d は期待している 2群間の平均値の差の大きさです。

例えば、標準偏差が10、2群間の平均値の差が10以上を期待するなら、式は次のようになり n は 16 です。

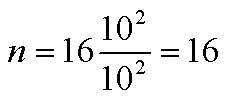
この2分の1の差でも検出したいなら、式は次のようになり、n は 4倍の 64 です。

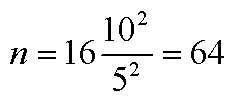
この式は、実験群、対照群、ともに n が等しいことを前提にしています。従って、実験全体では 2n 個のデータを採ることになります。