※コラム「統計備忘録」の記事一覧はこちら※

最小値が2、最大値が12の33個のデータがあったとします。33個のデータを小さい方から順に1番から33番まで番号を振っておきます。一本の定規の上に、各データを、データが持っている値と定規の目盛りが一致するように積み上げたところをイメージしてください。

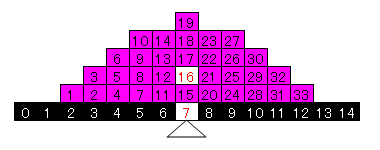
この定規（上図の黒い棒）の左右のバランスが取れるところ、この例では７が平均値です。平均値とはてこの原理における支点です。一方、中央値はデータの並びにおいてちょうど真ん中のところ、この例なら17番のデータの置かれた7が中央値になります。このように平均値を中心に左右均等に散らばる場合は平均値も中央値も同じになります。

それでは33番のデータの値が12ではなく45だったとしましょう。33番が右に大きくずれたことで、てこの原理が働いて平均値は8になります。平均値は外れ値の影響を受けやすいことが分かります。中央値は外れ値の影響を受けないので7のままです。

33番のデータの値が45ではなく450だったとしても中央値は同じですね。でも平均値は20を超えてしまいます。こうなると、33個中32個は平均値より下ということになってしまいます。 一方、中央値は、依然、7のままですね。中央値のこの性質のことを「外れ値に対してロバストである（頑健性がある）」と言います。

それでは次の図を見てください。この場合も平均値は７ですが、中央値は５になります。このように、平均値と中央値が異なるとき、分布は平均値より中央値側に偏りがあります。年収や資産など、お金についてのデータをとると平均値より中央値が低くなることが殆どです。

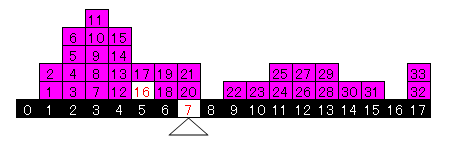
このような分布になると中央値にも、データを半々に分けるという意味しかありません。数値だけでデータの分布を把握しようとするなら、最小値と最大値ぐらいは少なくともみておきましょう。続いて、最小値から中央値までの幅（この例では6）、中央値から最大値までの幅（10）を比較します。幅の小さい方に分布が密集していることが分かります。これに第１四分位（25パーセンタイル）と第3四分位（75パーセンタイル）の数値も分かるとかなり正確に全体の分布を予測できます。この5つの数値を使ったデータ分布の表現を五数要約と言います。五数要約をグラフにしたのが箱ひげ図です。