- Step1. 基礎編
- 28. 等分散性の検定とWelchのt検定
28-2. F分布表
24-4章の「対応のない2標本t検定」で次のような問題について考えました。
例題:
ある学校の1組と2組の算数のテストの平均点を比較します。1組30人の平均点は75点、標準偏差は5点でした。2組32人の平均点は70点、標準偏差は8点でした。この結果から、1組と2組の算数のテストの平均点に差はあるでしょうか。
■t検定を行うための前提条件
この例題に対しては対応のない2標本t検定を行いましたが、t検定を行う場合には次のような条件が成り立つことを前提としています。これらの条件を満たさない場合、検定の結果に影響が出る場合があります。3番目の条件である「2つの母集団の母分散が等しいこと」については、F分布に従う統計量FとF分布表を使って検定できます。
- 標本は母集団からランダムに選ばれていること
- 母集団の分布は正規分布に従うこと
- 2標本t検定を行う場合には、2つの母集団の母分散が等しいこと
■F分布表の読み方
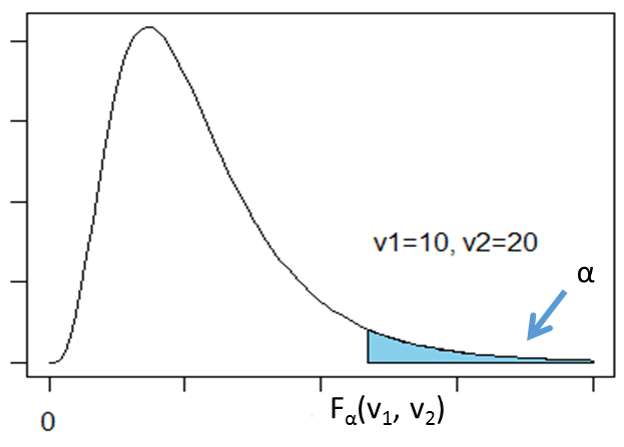
F分布は自由度によって分布の形が変わるため、統計数値表の読み方が標準正規分布表の場合と異なる点に注意しなければなりません。例えばF分布表に次のような図が描かれている場合、「自由度が(![]() ,
, ![]() )であるF分布において、水色部分の面積が
)であるF分布において、水色部分の面積が![]() となるFの値
となるFの値![]() ,
, ![]() 」を表します。
」を表します。
F分布表はいくつかの![]() の値ごとに作成されているので、まず該当する
の値ごとに作成されているので、まず該当する![]() の値について書かれた表を見ます。ここでは「
の値について書かれた表を見ます。ここでは「![]() 」の表を見てみます。
」の表を見てみます。
【![]() 】
】
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | 161.448 | 199.500 | 215.707 | 224.583 | 230.162 | 233.986 | 236.768 |
| 2 | 18.513 | 19.000 | 19.164 | 19.247 | 19.296 | 19.330 | 19.353 |
| 3 | 10.128 | 9.552 | 9.277 | 9.117 | 9.013 | 8.941 | 8.887 |
| 4 | 7.709 | 6.944 | 6.591 | 6.388 | 6.256 | 6.163 | 6.094 |
| 5 | 6.608 | 5.786 | 5.409 | 5.192 | 5.050 | 4.950 | 4.876 |
| 10 | 4.965 | 4.103 | 3.708 | 3.478 | 3.326 | 3.217 | 3.135 |
| 15 | 4.543 | 3.682 | 3.287 | 3.056 | 2.901 | 2.790 | 2.707 |
| 20 | 4.351 | 3.493 | 3.098 | 2.866 | 2.711 | 2.599 | 2.514 |
| 25 | 4.242 | 3.385 | 2.991 | 2.759 | 2.603 | 2.490 | 2.405 |
| 30 | 4.171 | 3.316 | 2.922 | 2.690 | 2.534 | 2.421 | 2.334 |
横軸が1つ目の自由度![]() を、縦軸が2つ目の自由度
を、縦軸が2つ目の自由度![]() を表しています。自由度が(5, 10)の場合、縦軸と横軸が交わった部分の値が自由度(5, 10)のときに
を表しています。自由度が(5, 10)の場合、縦軸と横軸が交わった部分の値が自由度(5, 10)のときに![]() となるF値です。この値は「3.326」であることが分かります。また、「
となるF値です。この値は「3.326」であることが分かります。また、「![]() 」と書きます。
」と書きます。
【![]() 】
】
| v2↓ v1→ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 161.448 | 199.500 | 215.707 | 224.583 | 230.162 | 233.986 | 236.768 |
| 2 | 18.513 | 19.000 | 19.164 | 19.247 | 19.296 | 19.330 | 19.353 |
| 3 | 10.128 | 9.552 | 9.277 | 9.117 | 9.013 | 8.941 | 8.887 |
| 4 | 7.709 | 6.944 | 6.591 | 6.388 | 6.256 | 6.163 | 6.094 |
| 5 | 6.608 | 5.786 | 5.409 | 5.192 | 5.050 | 4.950 | 4.876 |
| 10 | 4.965 | 4.103 | 3.708 | 3.478 | 3.326 | 3.217 | 3.135 |
| 15 | 4.543 | 3.682 | 3.287 | 3.056 | 2.901 | 2.790 | 2.707 |
| 20 | 4.351 | 3.493 | 3.098 | 2.866 | 2.711 | 2.599 | 2.514 |






