- Step1. 基礎編
- 28. 等分散性の検定とWelchのt検定
28-5. Welchのt検定
2標本t検定を行う場合、前提条件の1つとして「2つの母集団の分散が等しいこと」が必要です(28-2章参照)。そのため次の流れでt検定を行うという考え方があり、このように記載されている書籍もあります。
- 「等分散性の検定」で2標本の母分散が等しいかどうか検定(28-3章参照)
- 等分散ではないとは言えない場合(帰無仮説
 「2標本の母分散は等しい」が棄却されない場合)はt検定
「2標本の母分散は等しい」が棄却されない場合)はt検定 - 等分散ではないと言える場合(帰無仮説
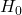 「2標本の母分散は等しい」が棄却される場合)はWelchのt検定(※後述します)
「2標本の母分散は等しい」が棄却される場合)はWelchのt検定(※後述します)
ただし、統計学では検定を繰り返し行うと「多重性の問題」が生じるため、最近では2標本のt検定を行う場合には等分散性の検定は行わず、等分散かどうかを考慮する必要のない「Welchのt検定」を行ったほうが良いという考え方も一般的になりつつあります。
■Welchのt検定
Welchのt検定は、2標本t検定と同様に平均値の差の検定方法です。2標本t検定とは異なり2標本の母分散が等しいとは限らない場合に使うことができます。2標本の検定においてWelchのt検定を行う場合の統計量tは次の式から求めます。1群目の標本平均を![]() 、サンプルサイズを
、サンプルサイズを![]() 、不偏分散を
、不偏分散を![]() 、2群目の標本平均を
、2群目の標本平均を![]() 、サンプルサイズを
、サンプルサイズを![]() 、不偏分散を
、不偏分散を![]() とします。
とします。
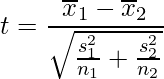
自由度![]() は次の近似式から算出された値を用います。非常に複雑な式ですが覚える必要はありません。この式を用いると自由度が整数ではなくなる場合があります。
は次の近似式から算出された値を用います。非常に複雑な式ですが覚える必要はありません。この式を用いると自由度が整数ではなくなる場合があります。
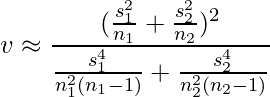
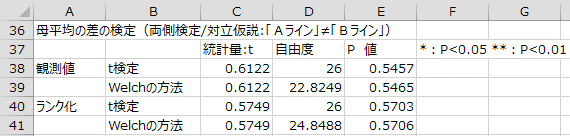
Rをはじめとする多くの統計ソフトでは、2標本t検定を行うとWelchのt検定の結果が算出されるようになっています。エクセル統計で母平均の差の検定を行うと、t検定の結果に加えてWelchのt検定の結果も出力されます。
【コラム】多重性の問題
多重性の問題とは「検定を複数回行うと、第1種の過誤の確率が大きくなる」という問題です。第1種の過誤については23-3章と23-4章で既に学びました。
例えば、A、B、Cと3つの薬剤があったとします。これらの薬効を調べるためにA-B、A-C、B-Cと2薬ずつ3組を有意水準5%でt検定したとします。帰無仮説![]() を「3剤に薬効の差はない」としても、それぞれの検定で「本当は帰無仮説
を「3剤に薬効の差はない」としても、それぞれの検定で「本当は帰無仮説![]() が正しいのに誤って帰無仮説
が正しいのに誤って帰無仮説![]() を棄却してしまう第1種の過誤」を犯す確率が5%あります。3組の検定うち1組でも有意になってしまう確率は14.26%まで上がってしまいます。
を棄却してしまう第1種の過誤」を犯す確率が5%あります。3組の検定うち1組でも有意になってしまう確率は14.26%まで上がってしまいます。
なぜ14.26%に上がってしまうかは次の計算によります。まず、それぞれの検定で正しい結果(有意にならない。P>0.05)が出る確率は 95%(=0.95)ですが、3つとも正しい結果が出るとなると0.95の3乗で0.8574となります。逆に、3つの検定で1つ以上有意になる確率は1-0.8574で14.26%ということになります。
このように複数回の検定を重ねることによって、本来設定していた有意水準でより誤判定してしまう確率が高まってしまうことを検定の多重性の問題と呼びます。多重性の問題が生じる場面では注意を払うことが必要です。
【コラム】ボンフェローニ法
多重性を考慮した検定を多重比較検定といいます。多重比較検定法の1つがボンフェローニ法です。ボンフェローニ法では、有意水準![]() のもとで
のもとで![]() 個の事象について検定を行う場合、誤って有意であると判定してしまう確率(第1種の過誤の確率)を抑えるため、新たに
個の事象について検定を行う場合、誤って有意であると判定してしまう確率(第1種の過誤の確率)を抑えるため、新たに ![]() を有意水準として検定を行います。
を有意水準として検定を行います。
ただし、事象![]() の数が大きくなると
の数が大きくなると![]() が非常に小さくなるため検出力が低下します。すなわち、ボンフェローニ法は有意になりにくい保守的な検定方法であるといえます。
が非常に小さくなるため検出力が低下します。すなわち、ボンフェローニ法は有意になりにくい保守的な検定方法であるといえます。
28. 等分散性の検定とWelchのt検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 24. 平均値の検定
24-3. 2標本t検定とは
- 24. 平均値の検定
24-4. 対応のない2標本t検定
- 統計解析事例
母平均の差の検定─エクセル統計による解析事例
- ブログ
Excelの分析ツール (3)






