※コラム「統計備忘録」の記事一覧はこちら※

「Excelの分析ツール (2)」の続き。残る５つの分析ツールですが、まずサンプリングからですね。

分析ツールのウィンドウ

サンプリング

入力済みの大量の数値データから標本抽出（サンプリング）を行うときに利用します。サンプリングの方法は「周期」と「ランダム」の2通りあります。「周期」は一定の間隔を空けてデータを取り出したいときに使用します。「ランダム」は無作為抽出（ランダムサンプリング）に利用します。
中心極限定理を実感してみたいなら、同じ分析ツールの中にある乱数発生の機能で大量のデータを作り、続いてこのサンプリング機能でランダムサンプリングを50回ほど繰り返し行ってみましょう。50個のサンプルの標本平均の分布は中心極限定理に従った正規分布を描くはずです。

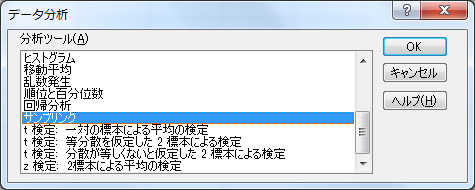
t検定：一対の標本による平均の検定

1つの個体からAとBの2つの条件下でデータを採取します。これを標本内のすべての個体より行います。A、B、いずれかのみというケースは許されず、必ず対になっている必要があります。続いてAとBの差を求め、この差の平均が統計的に有意かどうかを検定します。対応のあるデータのt検定（paired t-test）と呼ばれている検定手法です。

「仮説平均との差異」には何も入力しません（まず使うことはありません。何も入力しなければ「0」の扱いになります）。「α」には有意水準を設定します。初期値として「0.05（有意水準が5%ということ）」が設定されています。有意水準 1% で検定したいからといってわざわざ「0.01」と入力する必要はありません。この値は有意水準におけるt値の境界値を求めるだけのものです。有意差があるかどうかは、出力されたP値（片側、両側、それぞれに出力されます）を見れば事足ります。P値が自分の定めた有意水準のαより小さい場合に有意差ありと判断します。

ExcelのTTEST関数、T.TEST関数を用いる場合はTTEST関数の4番目の引数「検定の種類」を「1」に設定します。両側検定、片側検定の区別は3番目の引数「検定の指定」で行います。関数が返す値はP値のみになります。上記をTTEST関数を用い、両側検定を行うならワークシートのセルに次のように入力します。関数のデータはラベルを含めることができないので注意しましょう。

=TEST(C22:C28,D22:D28,2,1)

なお、条件が3つ以上あるなら、同じ分析ツール内の繰り返しのない二元配置分散分析を用いましょう。

エクセル統計で「t検定：一対の標本による平均の検定」を行うなら、[平均の推定・検定]メニューから[2群の母平均の差の検定(対応あり)]を選択してください。条件が3つ以上あるなら、データの書式に合わせて、[一元配置分散分析(対応あり)]か[多元配置分散分析(対応あり)]のいずれかを利用してください。

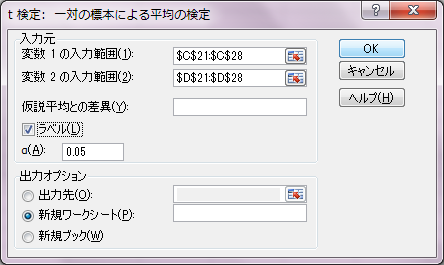
t検定：等分散を仮定した2標本による検定

いわゆるt検定のことです。対応のない2つの標本間で平均値の差を検定する場合に用います。対応のない2標本のt検定は、2標本の分散が等しいことを前提としているか、2標本の分散が等しくないとしているかで計算方法に違いがあります。後者は、Welchの方法によってｔ検定を行います。次に説明する「t検定：分散が等しくないと仮定した2標本による検定」がWelchの方法によるものです。なお、2標本の等分散性を検定するなら、さきほどのF検定を用います。「仮説平均との差異」、「α」については設定を気にする必要はありません。

ExcelのTTEST関数、T.TEST関数を用いる場合はTTEST関数の4番目のパラメータ「検定の種類」を「2」に設定します。

=TEST(C29:C37,D29:D35,2,2)

なお、条件が3つ以上あるなら、同じ分析ツール内の繰り返しのない二元配置分散分析を用いましょう。

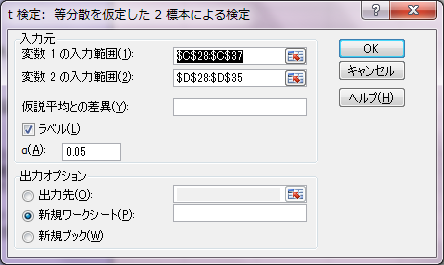
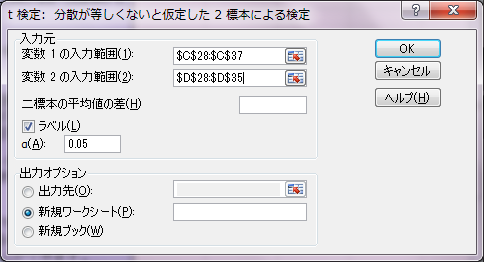
t検定：分散が等しくないと仮定した2標本による検定

Welchの方法によって2標本の平均の差のｔ検定を行います。先ほどのｔ検定は2標本が等分散であることを前提としています。しかしながら、片方の標本がもう片方の標本よりも平均も分散も大きくなるということがよくあります。また、等分散であるかどうか事前に想定できないこともよくあります。このような時は、Welchの方法によるｔ検定が適しています。

Welchの方法ではｔ分布の自由度に小数点以下の値が生じます。Excelの分析ツールでは、四捨五入後の自由度によるｔ分布を用いてP値を計算してしまいます。一方、ExcelのTTEST関数やT.TEST関数を使ってもWelchの方法によるｔ検定ができるのですが（関数の4番目の引数「検定の種類」を「3」に設定します）、関数から求められるP値は自由度を四捨五入しないで計算しています。より検定の精度を高めるなら、関数を使って検定を行った方が良いでしょう。

=TEST(C29:C37,D29:D35,2,3)

なお、エクセル統計で「F検定：2標本を使った分散の検定」と「t検定：等分散を仮定した2標本による検定」、「t検定：分散が等しくないと仮定した2標本による検定」を行う場合は、[平均の推定・検定]メニューから[2群の母平均の差の検定]を選択してください。1回の操作で3つの検定結果が同時に出力されます。

z検定：2標本による平均の検定

2標本の母分散が既知の場合や、大標本のデータで標本の分散と母分散が等しいと仮定できる場合は、正規分布を用いた平均の差の検定ができます。母分散が既知というと工場の品質管理データのように以前からの蓄積があったり、過去の大規模調査の結果を利用できたりという場面が考えられますが、このような既知の母分散を利用できる場合は、「変数1の分散（既知）」、「変数2の分散（既知）」に直接分散を入力します。分散が大きいと入力が大変ですから、できれば標準偏差の入力にしてほしいところです。

平均については「変数1の入力範囲」、「変数2の入力範囲」に指定したデータから計算します。分散の入力がなければ（母分散が未知の場合）、こちらも平均を求めるのに使ったデータから計算します。

ExcelにはZTEST関数やZ.TEST関数がありますが、1標本検定で、しかも、片側検定（標本平均が比較値より大きい場合のみ）のP値しか返してくれません。

エクセル統計では「z検定：2標本による平均の検定」も、[平均の推定・検定]メニューから[2群の母平均の差の検定]を利用します。1回の操作で3つの検定結果が同時に出力されます。「公式」のオプションを「正規分布」に変更するとz検定になります。ただし、母分散が未知の場合にのみ対応しています。母分散が既知の場合には分析ツールをご利用ください。

以上がExcelの分析ツールに搭載されている18種の統計解析手法です。

私がはじめてExcelの分析ツールを使ってみたのは1995年のことですが、その後、Excelのバージョンが変わってもExcelの分析ツールのメニューには一切変化がありませんでした。さすがに20年近く経つと統計解析のトレンドも随分と変わってしまいましたので、実用性という面では価値が薄くなってきています。せめて、独立性の検定（カイ二乗検定）や基本的なノンパラメトリック検定の幾つかは組み込んで欲しいところです。

それから、Excelの統計用語は一般的でないものが多く、また、ヘルプの説明が説明になっていない点も要注意です。統計学の知識が中途半端だとExcelの分析ツールも統計関数も使いこなすのが困難です。Excelを利用して統計学を学ぶ本は毎年のように出版されていますから、統計学の初心者は1冊持っていた方が安心でしょう。