※コラム「統計備忘録」の記事一覧はこちら※

今回のコラムを書いていて不思議に思ったのは分析ツールのリストの並びです。リストは分散分析に始まって ｔ検定、ｚ検定で終わります。「分散分析も、ｔ検定と ｚ検定も、平均が同じかどうかを検定するためにあるのに、何故、リストの両端に分かれているの？」、「時系列データの平滑化に使う指数平滑と移動平均の間にF検定やヒストグラムが入るのはどうして！」といったところです。英語版を見れば一目瞭然ですが、この並びは ANOVA から z test までと分析手法の英語名によるアルファベット順なのです。Descriptive Statistics が「記述統計量」でなく「基本統計量」と訳されているので、謎解きに手間取ってしまいました。

さて、「Excelの分析ツール (1)」の続きです。

分析ツールのウィンドウ

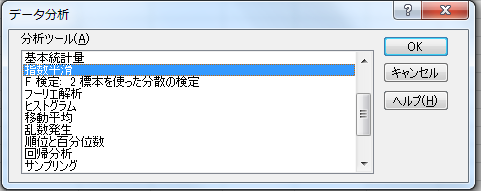
指数平滑

指数平滑という手法を使って、時系列データの平滑化を行います。ダイアログでは「減衰率」を設定するようになっていますが、この減衰率には（1-平滑化係数）の値を設定します。

F検定：2標本を使った分散の検定

2変数のデータ範囲を指定し、「変数1の分散＞変数2の分散（観測された分散比が 1 より大きい）」ならF分布の上側による片側検定を、「変数1の分散＜変数2の分散（観測された分散比が 1 より小さい）」なら下側による片側検定を行います。2変数のどちらの分散が大きいかによって対立仮説が変更されてしまうので注意が必要です。なお、ここで出力される P値を 2倍すると両側検定の P値となり、FTEST関数による P値と等しくなります。

フーリエ解析

高速フーリエ変換(FFT)と逆変換を行います。フーリエ解析については、ほとんど知識がありませんのでコメントは控えさせていただきます。

ヒストグラム

量的データを読み込んでヒストグラムを作るためにあるんですが、オプションの「グラフ」をチェックしないと度数分布表しか出力しないので要注意です。度数分布表の作り方も一般的じゃありません。度数分布表の各階級は「○○以上-◇◇未満」とするのが普通ですが、Excelの分析ツールは「○○より大きい-◇◇以下」となっています。それから、出力されるグラフはただの棒グラフですヒストグラムらしくするにはグラフの書式設定で「棒の間隔」に「0」を入力します。分析ツールによりヒストグラムの作成することはお奨めしません。COUNTIF関数やグラフの編集の仕方をマスターした方が良いでしょう。

移動平均定

移動平均という手法を使って、時系列データの平滑化を行います。分析ツールの移動平均は株価チャートで使われる移動平均と同じ計算原理です。「区間（N)」に5を指定した場合、ある時点tの移動平均は、t-4、t-3、t-2、t-1、t の5時点のデータの平均になります。本来の移動平均では、ある時点ｔの移動平均は、t-2、t-1、t、t+1、t+2 とその前後の時点のデータを使って求めます。そのため、区間が奇数か偶数かでも計算方法が異なります。

乱数発生

ExcelにはRAND関数とRANBETWEEN関数の2種類の乱数を発生させる関数がありますが、一様分布の乱数しか作れない、シードを設定できないので再現性が無いといった弱点があります。また、ワークシートに何か入力するたびに乱数の値が変わってしまうという点もやっかいです。分析ツールでは、均一、正規、ベルヌーイ、二項、ポワソン、離散の6種類の分布から乱数を選ぶことができます（分布のリストにはパターンというのがありますが、これは乱数ではありません）。

順位と百分位数

RANK関数とPERCENTRANK関数が使えれば必要ありません。

回帰分析

重回帰分析もできます。標準偏回帰係数が出力されない、説明変数が16個までしか分析できない、変数選択ができない、欠損値があると分析できない、用語が一般的ではないといった使用上の注意点が幾つかあります。