Step1. 基礎編
28. 等分散性の検定とWelchのt検定

28-4. 等分散性の検定

例題：

ある学校の1組と2組の国語のテストの平均点を比較します。1組26人の平均点は60点、不偏分散は20でした。2組31人の平均点は65点、不偏分散は15でした。この結果から、1組と2組の国語のテストの点数の分散は等しいといえるでしょうか。

仮説を立てる

帰無仮説 $H_{0}$ は「1組と2組の国語のテストの点数の分散は等しい」とします。したがって、対立仮説 $H_{1}$ は「1組と2組の国語のテストの点数の分散は等しくない」となります。

有意水準を設定する

$\alpha$ ＝0.10とします。

適切な検定統計量を決める

等分散性の検定を行うことから、統計量Fを使います。統計量Fは次の式から求めます。 $s_{1}^{2}$ は1群目の不偏分散、 $s_{2}^{2}$ は2群目の不偏分散を表します。等分散性の検定においてF統計量を算出するときには2つの分散のうち、大きな値の方を分子にします。この例題では $s_{1}^{2}$ =20（1組）、 $s_{2}^{2}$ =15（2組）となります。

$\displaystyle F=\frac{s_{1}^{2}}{s_{2}^{2}}$

棄却ルールを決める

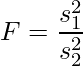
この検定で使用する分布は自由度「( $k_{1}$ , $k_{2}$ )=(26-1, 31-1)=(25, 30)」の「F分布」です。2つの分散が等しいかどうかを検定するので、両側検定を行います。このとき、統計数値表を参照する際に用いる $\alpha$ の値は、設定した有意水準である0.1を2で割った値の $\alpha$ =0.05となる事に注意してください。統計数値表から $F_{0.05}(25, 30)$ の値を読み取ると「 $F_{0.05}(25, 30)=1.878$ 」となっています。また、反対側の値は「 $F_{0.05}(30, 25)=1.919$ 」の逆数を取って「 $F_{0.95}(25, 30)=0.521$ 」となります。

※確率変数 $X$ が自由度（ $k_{1}, k_{2}$ ）のF分布に従う時、その逆数である $\displaystyle \frac{1}{X}$ は自由度（ $k_{2}, k_{1}$ ）のF分布に従います。したがって、自由度（ $k_{1}, k_{2}$ ）のF分布における上側 $100\alpha\%$ 点の値が $F_{\alpha}(k_{1}, k_{2})$ のとき、自由度（ $k_{2}, k_{1}$ ）のF分布における下側 $100\alpha\%$ 点の値は $\displaystyle F_{1-\alpha}(k_{2}, k_{1}) = \frac{1}{F_{\alpha}(k_{1}, k_{2})}$ として算出できます。

検定統計量を元に結論を出す

$\displaystyle F=\frac{s_{1}^{2}}{s_{2}^{2}}=\frac{20}{15}=1.33$

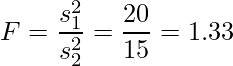
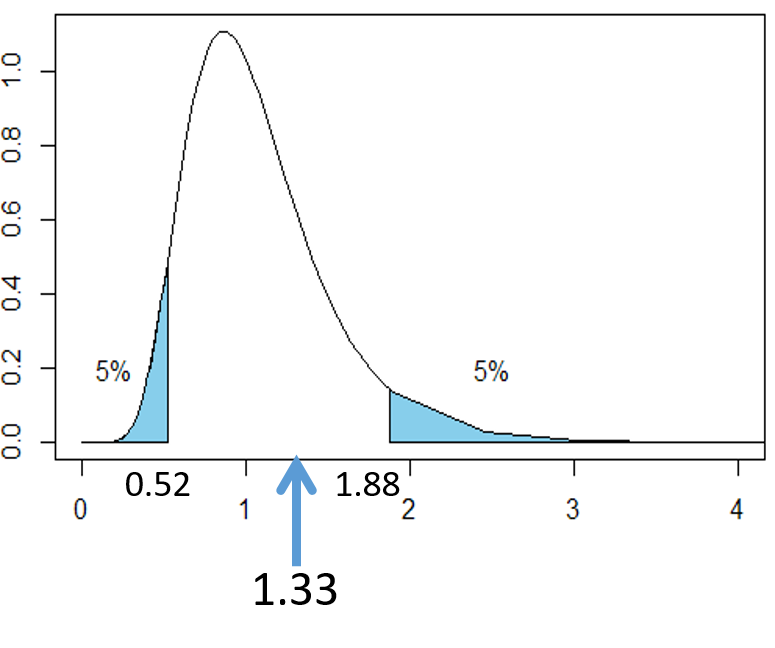
次の図は自由度(25, 30)のF分布を表したものです。F=1.33は図の矢印の部分に該当します。矢印は棄却域に入っていないことから、「有意水準10%において、帰無仮説 $H_{0}$ は棄却されない」という結果になります。つまり、「1組と2組の国語のテストの点数の分散は等しくないとは言えない」と結論づけられます。