28. 等分散性の検定とWelchのt検定

練習問題（28. 等分散性の検定とWelchのt検定）

F分布表が必要な場合、下の表を用いてよい。

F分布に関する次の記述のうち正しいものを選べ。

F分布はt分布やカイ二乗分布と同様、1つの自由度から分布の形が決まる。
母分散の信頼区間を求めるときに使うのはF分布である。
F分布のグラフは左右対称である。
分散分析はF分布を用いて検定を行う。

答えを見る

答え閉じる

×：F分布は2つの自由度から分布の形が決まります。
×：母分散の信頼区間を求めるときに使うのはカイ二乗分布です。
×：F分布のグラフは左右対称ではなく、右に裾を引く形です。
◯：正しいです。分散分析ではF分布を用いて検定を行います。

F分布表から、それぞれの自由度が(5, 3)の場合の上側確率2.5％点の値を求めよ。

答えを見る

答え閉じる

自由度が(5, 3)の場合、横軸は1つ目の自由度である「5」の列を、縦軸が2つ目の自由度である「3」の行を参照します。縦軸と横軸が交わった部分の値が自由度(5, 3)のときに 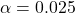$\alpha=0.025$ となるF値で、「14.885」であると読み取れます。

上側確率 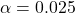$\alpha=0.025$ のF分布表

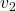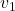$v_{2}$ ↓ $v_{1}$ →	1	2	3	4	5	6	7
1	647.789	799.500	864.163	899.583	921.848	937.111	948.217
2	38.506	39.000	39.165	39.248	39.298	39.331	39.355
3	17.443	16.044	15.439	15.101	14.885	14.735	14.624
4	12.218	10.649	9.979	9.605	9.364	9.197	9.074
5	10.007	8.434	7.764	7.388	7.146	6.978	6.853

F分布表から、それぞれの自由度が(6, 15)の場合の上側確率5％点の値を求めよ。

答えを見る

答え閉じる

自由度が(6, 15)の場合、横軸は1つ目の自由度である「6」の列を、縦軸が2つ目の自由度である「15」の行を参照します。縦軸と横軸が交わった部分の値が自由度(6, 15)のときに 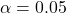$\alpha=0.05$ となるF値で、「2.790」であると読み取れます。

上側確率 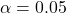$\alpha=0.05$ のF分布表

v2↓　v1→	1	2	3	4	5	6	7
1	161.448	199.500	215.707	224.583	230.162	233.986	236.768
2	18.513	19.000	19.164	19.247	19.296	19.330	19.353
3	10.128	9.552	9.277	9.117	9.013	8.941	8.887
4	7.709	6.944	6.591	6.388	6.256	6.163	6.094
5	6.608	5.786	5.409	5.192	5.050	4.950	4.876
10	4.965	4.103	3.708	3.478	3.326	3.217	3.135
15	4.543	3.682	3.287	3.056	2.901	2.790	2.707
20	4.351	3.493	3.098	2.866	2.711	2.599	2.514

分散未知の正規分布に従う2群からサンプリングし、次のような結果を得た。この2群の母分散は等しいと考えられるかを有意水準0.05で検定せよ。

項目	A群	B群
サンプルサイズ	11	8
不偏分散	1.03	4.30
分散	0.94	3.76

答えを見る

答え閉じる

等分散性の検定における帰無仮説 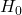$H_0$ は「2つの群の母分散は等しい」です。最初に検定統計量であるF統計量を求めます、統計量Fは不偏分散の比となる事に注意してください。

$F= \displaystyle \frac{4.30}{1.03} =4.17...$

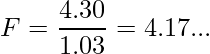
分子の自由度は7、分母の自由度は10となるので、F(7, 10)の2.5％点を表から読み取ります。 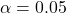$\alpha=0.05$ の値ではなく、有意水準0.05を2で割った 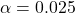$\alpha=0.025$ での値となるのがポイントです。この値は「3.950」で統計量Fの方が大きいため、帰無仮説 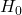$H_0$ を棄却し「2つの群の母分散は等しくない」と結論付けられます。

分散未知の正規分布に従う2群からサンプリングし、次のような結果を得た。この2群の母分散は等しいと考えられるかを有意水準0.05で検定せよ。

項目	A群	B群
サンプルサイズ	5	6
分散	4.00	7.00

答えを見る

答え閉じる

等分散性の検定における帰無仮説 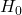$H_0$ は「2つの群の母分散は等しい」です。最初に検定統計量である統計量Fを求めます。統計量Fは不偏分散の比となる事に注意してください。

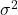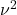この問題では、不偏分散がなく分散しか与えられていないため、まず不偏分散を求める必要があります。分散 $\sigma ^2$ と不偏分散 $\nu ^2$ には次の関係が成立します。

$\displaystyle \nu ^2 =\frac{n}{n-1} \sigma ^2$

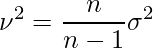
従って、分散を 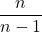$\displaystyle \frac{n}{n-1}$ 倍すれば、不偏分散を求められることが分かります。これを用いて統計量Fを計算すると、次のようになります。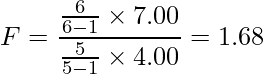

$F= \displaystyle \frac{\frac{6}{6-1} \times 7.00}{\frac{5}{5-1} \times 4.00} =1.68$

分子の自由度は5、分母の自由度は4となるので、F(5, 4)の2.5％点を表から読み取ります。また、また、反対側の値は「F(4, 5)の2.5％点」の逆数を取った値となります。 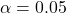$\alpha=0.05$ の値ではなく、有意水準0.05を2で割った 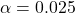$\alpha=0.025$ での値となるのがポイントです。

これらの値は「9.364」と「0.135(=1/7.388)」で 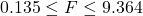$0.135 \leq F \leq 9.364$ となることから、帰無仮説 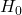$H_0$ は棄却できず「2つの群の母分散は等しくないとは言えない」と結論付けられます。

上側確率 $\alpha=0.05$ のF分布表

$v_{2}$ ↓ $v_{1}$ →	1	2	3	4	5	6	7
1	161.448	199.500	215.707	224.583	230.162	233.986	236.768
2	18.513	19.000	19.164	19.247	19.296	19.330	19.353
3	10.128	9.552	9.277	9.117	9.013	8.941	8.887
4	7.709	6.944	6.591	6.388	6.256	6.163	6.094
5	6.608	5.786	5.409	5.192	5.050	4.950	4.876
10	4.965	4.103	3.708	3.478	3.326	3.217	3.135
15	4.543	3.682	3.287	3.056	2.901	2.790	2.707
20	4.351	3.493	3.098	2.866	2.711	2.599	2.514
25	4.242	3.385	2.991	2.759	2.603	2.490	2.405
30	4.171	3.316	2.922	2.690	2.534	2.421	2.334

上側確率 $\alpha=0.025$ のF分布表

$v_{2}$ ↓ $v_{1}$ →	1	2	3	4	5	6	7
1	647.789	799.500	864.163	899.583	921.848	937.111	948.217
2	38.506	39.000	39.165	39.248	39.298	39.331	39.355
3	17.443	16.044	15.439	15.101	14.885	14.735	14.624
4	12.218	10.649	9.979	9.605	9.364	9.197	9.074
5	10.007	8.434	7.764	7.388	7.146	6.978	6.853
10	6.937	5.456	4.826	4.468	4.236	4.072	3.950
15	6.200	4.765	4.153	3.804	3.576	3.415	3.293
20	5.871	4.461	3.859	3.515	3.289	3.128	3.007
25	5.686	4.291	3.694	3.353	3.129	3.969	2.848
30	5.568	4.182	3.589	3.250	3.026	2.867	2.746